Ситекторът на триъгълник - какво е това?

Геометрията е една от най-сложните и сложни науки. В него това, което изглежда очевидно на пръв поглед, рядко се оказва правилно. Бисекторите, височините, медианите, проекциите, тангентите са огромен брой наистина трудни термини, с които лесно се бърка.

Всъщност, с правилното желание, можете да разберете теорията на всяка сложност. Когато става въпрос за bisector, медиана и височина, трябва да се разбере, че те не са характерни за триъгълници. На пръв поглед това са прости линии, но всеки от тях има свои свойства и функции, познаването на които значително опростява решението на геометричните проблеми. И така, какво е ъглоположник на триъгълник?

дефиниция

Терминът "бисектрис" идва от комбинация от латински думи "два" и "изрязани", "нарязани", които индиректно показва нейните свойства. Обикновено, когато децата се запознават с този лъч, те се умоляват да запомнят кратка фраза: "Екосекторът е плъх, който се движи по ъглите и наполовина прави ъгъла". Естествено, такова обяснение не е подходящо за по-възрастните ученици, освен това те обикновено не се питат за въглища, а за геометрична форма. Така бисектрисата на триъгълник е лъч, който свързва върха на триъгълника с противоположната страна, като разделя ъгъла на две равни части. Точката на противоположната страна, на която се намира бисектриса, за произволен триъгълник, се избира случайно.

Основни функции и свойства

Основните свойства на този лъч малко. Първо, защото ситекторът на триъгълник разделя ъгъла на половина, всяка точка, лежаща върху нея, ще бъде на еднакво разстояние от страните, образуващи върха. Второ, във всеки триъгълник може да се изчертаят три бисектриси, според броя на наличните ъгли (затова вече ще има четири от тях в същия четириъгълник и т.н.). Точката, в която се пресичат всичките три лъча, е център на кръг, вписан в триъгълник.

Свойствата са сложни

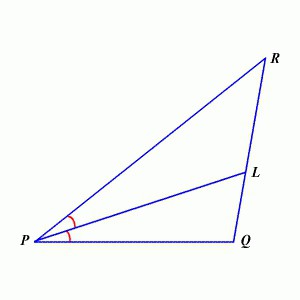
Нека усложним теорията малко. Друго интересно свойство: ситекторът на ъгъла на триъгълника разделя противоположната страна на сегменти, чието съотношение е равно на съотношението на страните, образуващи върха. На пръв поглед това е трудно, но всъщност всичко е просто: в предложената цифра, RL: LQ = PR: PK. Между другото, това свойство се нарича теорема за бисектриса и се появява за първи път в произведенията на древногръцкия математик Евклид. Спомняха го в един от руските учебници едва през първата четвърт на XVII век.

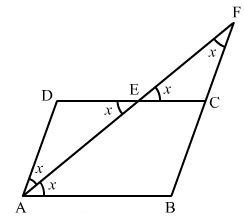
Малко по-трудно. В четириъгълника ситекторът прекъсва равнобедрен триъгълник. Тази фигура показва всички равни ъгли за средната AF.

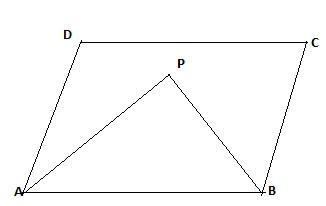
Освен това, в четириъгълници и трапеции, ъглополовите ъгли са перпендикулярни един на друг. На чертежа ъгълът на APB е 90 градуса.

В равнобедрен триъгълник

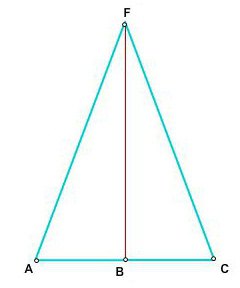
Равнобедрените на равнобедрен триъгълник е много по-полезен лъч. Това е в същото време не само разделител на ъгъла на половина, но също и медиана и височина.

Медианата е сегмент, който излиза от определен ъгъл и попада в средата на противоположната страна, като го разделя на равни части. Височината е перпендикулярна от върха към противоположната страна, с чиято помощ всяка задача може да бъде сведена до простата и примитивна питагорова теорема. В тази ситуация, симулатора на триъгълника е равен на корена на разликата между квадрата на хипотенузата и другия крак. Между другото, именно това свойство най-често се среща в геометричните проблеми.

За да се определи: в този триъгълник, bisector FB е медиана (AB = BC) и височина (ъглите на FBC и FBA са 90 градуса).

По принцип

И така, какво трябва да помните? Стрелата на триъгълника е лъч, който разделя горната част на половината. В пресечната точка на трите лъча е центърът на кръга, вписан в този триъгълник (единственият недостатък на това свойство е, че няма практическа стойност и служи само за правилното изпълнение на чертежа). Той разделя и противоположната страна на сегменти, чието съотношение е равно на съотношението на страните, между които е преминал този лъч. В четириъгълник свойствата са малко по-сложни, но, за да признаем, те практически не се срещат в задачи на ниво училище и затова обикновено не са засегнати от програмата.

Стрелата на един равнобедрен триъгълник е крайната мечта на всеки ученик. В същото време е средна (т.е. разделя противоположната страна на половина) и височина (перпендикулярна на тази страна). Решаването на проблеми с такъв бисектрис се свежда до питагоровата теорема.

Познаването на основните функции на бисектъра, както и неговите основни свойства, е необходимо за решаване на геометрични проблеми както на средно, така и на високо ниво на сложност. Всъщност, този лъч се намира само в планиметрията, така че е невъзможно да се каже, че запаметяването на информация за него ще позволи да се справят с всички видове задачи.