Период на колебание: експерименти, формули, задачи

Какъв е периодът на колебание? Каква е тази стойност, какво физическо чувство има тя и как да я изчислим? В тази статия ще разгледаме тези въпроси, разгледаме различните формули, чрез които можете да изчислите периода на трептене, както и да разберете каква връзка съществува между такива физични величини като периода и честотата на трептене на тялото / системата.

Определение и физически смисъл

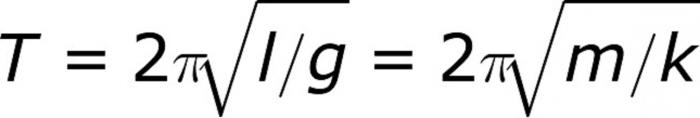
Периодът на колебание се нарича такъв период, в който тялото или системата изпълнява едно колебание (задължително завършено). Успоредно с това е възможно да се отбележи параметърът, при който колебанието може да се счита за завършено. Ролята на такова условие е връщането на тялото в първоначалното му състояние (към първоначалната координата). Много добра аналогия с периода на функцията. Между другото, грешка е да се мисли, че то се случва изключително в обикновената и висшата математика. Както знаете, тези две науки са неразривно свързани. Периодът на функциите може да се срещне не само при решаване на тригонометрични уравнения, но и в различни раздели на физиката, а именно, говорим за механика, оптика и др. При прехвърляне на периода на колебания от математика към физика е необходимо да се разбере само физическа величина (а не функция), която е пряко зависима от времето на преминаване.

Какви са колебанията?

Осцилациите са разделени на хармонични и ангармонични, както и периодични и непериодични. Би било логично да се приеме, че в случая на хармонични колебания те се изпълняват според някаква хармонична функция. Тя може да бъде едновременно синус и косинус. В този случай може да има коефициенти на разтягане и увеличаване-намаляване. Също така, трептенията са потиснати. Тоест, когато дадена сила действа върху системата, която постепенно “забавя” самите трептения. В същото време периодът става по-малък, а честотата на трептенията постоянно се увеличава. Много добре демонстрира такава проста аксиома на физическия опит с използването на махало. Може да бъде от пролетен тип, както и математически. Няма значение. Между другото, периодът на колебание в такива системи ще се определя от различни формули. Но повече за това по-късно. Сега даваме примери.

Опит с махала

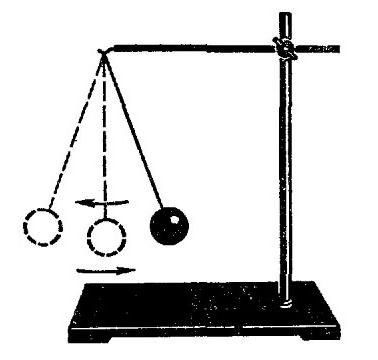
Всяко махало може да бъде взето първо, няма да има разлика. Законите на физиката и законите на физиката, че те се спазват във всеки случай. Но по някаква причина повече прилича на математическото махало. Ако някой не знае какво е: това е топка върху неразтегаема нишка, която е прикрепена към хоризонтална лента, прикрепена към краката (или елементи, които играят ролята си - да поддържат системата в равновесие). Топката е най-добре да се вземе от метала, така че опитът да е по-ясен.

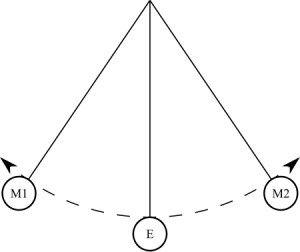
Така че, ако извадите такава система от равновесие, нанесете някаква сила на топката (с други думи, натиснете го), тогава топката ще започне да се люлее на нишката, следвайки определена траектория. С течение на времето ще забележите, че траекторията, по която минава топката, намалява. В същото време, топката започва да се движи напред и назад по-бързо и по-бързо. Това предполага, че честота на трептенията се увеличава. Но времето, за което топката се връща в първоначалното си положение, намалява. Но времето на едно пълно колебание, както открихме по-рано, се нарича период. Ако една стойност намалява, а другата се увеличава, тогава говорим за обратна пропорционалност. Така стигнахме до първата точка, въз основа на която се изграждат формулите за определяне на периода на трептене. Ако вземем пружинното махало, тогава законът ще се наблюдава там в малко по-различна форма. За да бъде най-ясно представено, ще приведем системата в движение във вертикална равнина. За да стане по-ясно, на първо място си струва да се каже какво е пролетното махало. От името е ясно, че в неговия дизайн трябва да има пролет. И това е вярно. Отново имаме хоризонтална равнина на опорите, към която е окачена пружина с определена дължина и твърдост. За нея, от своя страна, е спряно тегло. Тя може да бъде цилиндър, куб или друга фигура. Може дори да е нещо от трета страна. Във всеки случай, при премахване на системата от равновесното положение, тя ще започне да прави затихващи колебания. Най-ясно видимото увеличение на честотата е във вертикална равнина, без никакво отклонение. При това с експериментите можете да приключите.

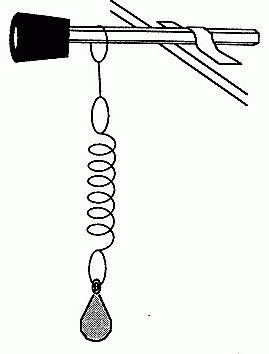
Така, в техния курс, открихме, че периодът и честотата на осцилациите са две физични величини, които имат обратна връзка.

Обозначаване на количества и размери

Обикновено периодът на колебание се обозначава с латинската буква Т. Много по-рядко може да се обозначава по различен начин. Честотата се обозначава с буквата µ (“Mu”). Както казахме в самото начало, периодът не е нищо повече от едно време, в което в системата настъпва пълно колебание. Тогава размерът на периода ще бъде втори. И тъй като периодът и честотата са обратно пропорционални, тогава размерът на честотата ще бъде разделен на секунда. В записите за задачи всичко ще изглежда така: T (s), µ (1 / s).

Формула за математическото махало. Проблем номер 1

Както и в случая с експерименти, реших първо да се справя с математическото махало. Ние няма да навлизаме в деривацията на формулата в детайли, тъй като такава задача не е била първоначално зададена. А самото заключение е тромаво. Но нека погледнем сами формулите, да разберем какви са ценностите в тях. Така че формулата за периода на трептене на математическото махало е както следва:

Където l - дължината на нишката, n = 3.14, и g - ускорение свободно падане (9.8 m / s ^ 2). Формулата не трябва да създава никакви трудности. Следователно, без допълнителни въпроси, пристъпваме незабавно към решаване на проблема за определяне на периода на колебание на математическото махало. Метална топка с тегло 10 грама е окачена на неразтегната нишка с дължина 20 сантиметра. Изчислете периода на трептене на системата, като го вземете като математическо махало. Решението е много просто. Както при всички проблеми във физиката, необходимо е да се опрости колкото се може повече поради отхвърлянето на ненужни думи. Те са включени в контекста, за да объркат решаващият, но всъщност те нямат абсолютно никакво тегло. В повечето случаи, разбира се. Тук можете да изключите момента с “неразтворима нишка”. Тази фраза не трябва да влиза в ступор. И тъй като имаме математическо махало, не бива да се интересуваме от масата на товара. Това означава, че думите около 10 грама са просто предназначени да объркат ученика. Но знаем, че във формулата няма маса, така че с чиста съвест можем да пристъпим към решението. Така че, ние приемаме формулата и просто заместваме стойностите в нея, тъй като е необходимо да се определи периода на системата. Тъй като не са уточнени допълнителни условия, ще закръглим стойностите до третия знак след десетичната запетая, както е обичайно. Като умножим и разделим стойностите, получаваме, че периодът на колебание е 0.886 секунди. Проблемът е решен.

Формула за пружинното махало. Проблем номер 2

Формулите на махалата имат обща част, а именно 2p. Тази стойност присъства в две формули едновременно, но те се различават по радикален израз. Ако в задачата за периода на пружинното махало се посочва теглото на товара, то тогава е невъзможно да се избегнат изчисления с неговото прилагане, какъвто беше случаят с математическото махало. Но не трябва да се страхувате. Ето формулата за периода на пролетното махало:

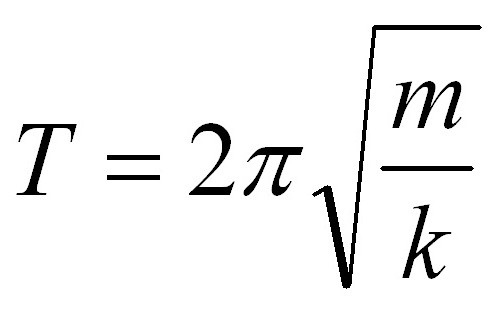
В него m е масата на товара, окачена от пружината, k е константата на пружината. В задачата може да се даде стойността на коефициента. Но ако във формулата на математическото махало не се разкривате особено - в крайна сметка 2 от 4 стойности са константи - тогава се добавя 3 параметър, който може да се промени. И на изхода имаме 3 променливи: периодът (честотата) на трептенията, пружинната константа на пружината, масата на окачения товар. Задачата може да бъде ориентирана към намиране на някой от тези параметри. Би било твърде лесно да погледнем отново за определен период от време, така че ще променим малко състоянието. Намерете коефициента на твърдост на пружината, ако общото време на трептене е 4 секунди, а теглото на пружинното махалово натоварване е 200 грама.

За да се реши всеки физически проблем, би било добре първо да начертаете картина и да напишете формули. Тук са половината от битката. При писане на формула е необходимо да се изрази коефициентът на коравина. Ние го имаме под корена, така че ще спрем двете страни на уравнението. За да се отървете от фракцията, умножете частите с k. Сега оставяме само коефициента от лявата страна на уравнението, т.е. разделяме частите на T ^ 2. По принцип, задачата може да бъде малко по-трудна, без да се определя периодът в цифрите, а честотата. Във всеки случай, при изчисляване и закръгляване (ние се съгласихме да закръглим до третия знак след десетичната запетая), се оказва, че k = 0, 157 N / m.

Периодът на свободните трептения. Формулата на периода на свободните трептения

По формулата за периода свободни вибрации разберете формулите, които сме подредили в предишните две проблеми. Съставено е и уравнението на свободните вибрации, но ние вече говорим за измествания и координати, и този въпрос се отнася до друга статия.

Съвети за решаване на проблеми, свързани с периода

1) Преди да започнете задача, запишете формулата, която е свързана с нея.

2) Най-простите задачи не изискват снимки, но в изключителни случаи те трябва да бъдат направени.

3) Опитайте се да се отървете от корените и знаменателите, ако е възможно. Уравнението, написано в ред, без знаменател, е много по-лесно и по-лесно да се реши.