Логаритми: правила, основни свойства и формули

Логаритмите и правилата на действията с тях са доста обемни и прости. Затова, за да разберете тази тема, няма да ви е трудно. След като научите всички правила на естествените логаритми, всеки проблем ще бъде решен самостоятелно. Първото запознаване с тази тема може да изглежда скучно и безсмислено, но с помощта на логаритми бяха решени много проблеми на математиците от 16-ти век. - За какво става въпрос? - помисли си. Прочетете статията до края и разберете, че този раздел на "Царицата на науките" може да представлява интерес не само за математиците, учените от точните науки, но и за обикновените ученици от средните училища.

Определение на логаритъма

Да започнем с дефиницията на логаритъма. Както много учебници казват: логаритъмът на числото b на база a (log _a b) е определено число c, за което това равенство притежава: b = a ^c . Тоест, с прости думи, логаритъмът е определена степен, в която ние изграждаме база, за да получим дадено число. Но е важно да се помни, че логаритъмът на формата log _a b има смисъл само когато: a> 0; а е номер, различен от 1; b> 0, следователно заключаваме, че логаритъмът може да бъде намерен само за положителни числа.

Класификация на логаритми по база

Логаритмите могат да бъдат всяко положително число в основата. Но има и два вида: естествени и десетични логаритми.

• Естественият логаритъм - логаритъмът с база e (e е номерът на Ойлер, чийто брой е приблизително равен на 2.7, ирационалният номер, който е въведен за експоненциалната функция y = e ^x ), се обозначава с ln a = log _e a;
• Десетичната логаритъм е логаритъм с база 10, т.е. log ₁₀ a = lg a.

Основни правила на логаритми

Първо трябва да се запознаете с основната логаритмична идентичност: ^{log _a b} = b, след това следвайте тези две основни правила:

• log _a 1 = 0 - тъй като всяко число в нулевата степен е 1;
• log _a a = 1.

Благодарение на откриването на логаритъма, не е трудно за нас да решим абсолютно всяко експоненциално уравнение, чийто отговор не може да се изрази в естествени числа, а само ирационално. Например: 5 ^x = 9, x = log ₅ 9 (тъй като няма естествено x за това уравнение).

Действия с логаритми

• log _a (x · y) = log _a x + log _a y - за да намерите логаритъма на продукта, трябва да добавите логаритмите на факторите. Имайте предвид, че основите на логаритмите са еднакви. Ако напишем това в обратен ред, ще получим правилото за добавяне на логаритми.
• log _a xy = log _a x - log _a y - за да намерите логаритъма на конкретното, трябва да намерите разликата между логаритмите на дивидента и делителя. Моля, обърнете внимание: логаритмите имат една и съща база. Когато пишем в обратен ред, получаваме правилото за изваждане на логаритми.

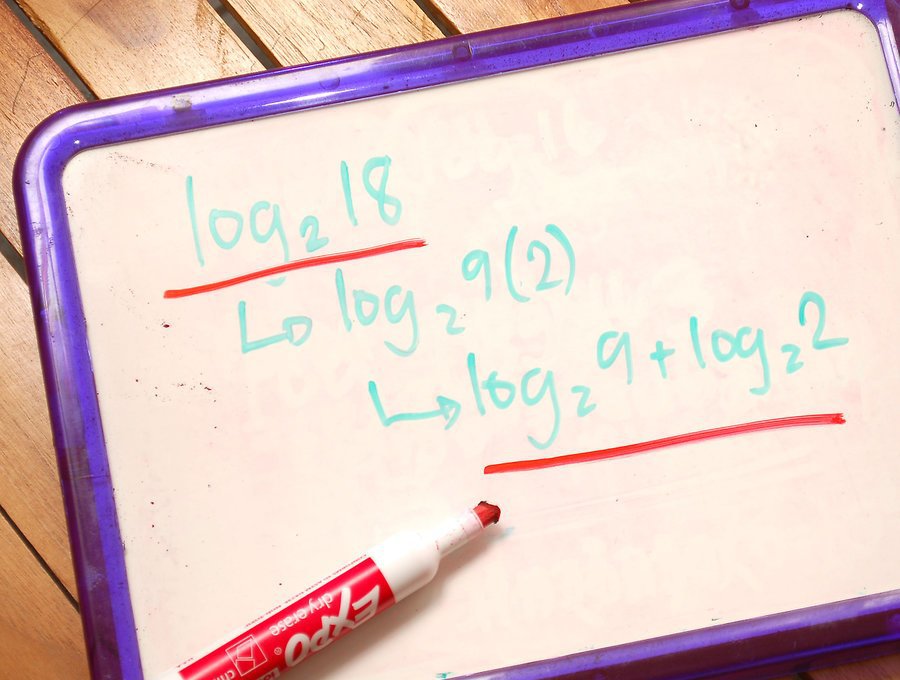
• log _{a ^k} x ^p = (p / k) * log _a x - по този начин, ако има аргументи и основи на логаритъма, те могат да бъдат извадени от логаритмичния знак.
• log _a x = log _{a ^c} x ^c е специален случай на предишното правило, когато експонентите са равни, те могат да бъдат намалени.
• log _a x = (log _b x) (log _b a) е така наречения преходен модул, процедурата за конвертиране на логаритъма в друга база.
• log _a x = 1 / log _x a е специален случай на преход, промяна на местата на базата и дадено число. Цялото изражение, образно казано, се обръща и логаритъмът с новата база се появява в знаменателя.

История на логаритми

През 16 век е необходимо да се извършат много приблизителни изчисления за решаване на практически задачи, главно в астрономията (например определяне на местоположението на кораба от Слънцето или звездите).

Тази необходимост нарастваше бързо и значителна трудност създаваше умножение и разделяне на многоцифрени числа. Математичният математик Напиер решил да замени трудоемкото умножение с обикновена добавка за тригонометрични изчисления, сравнявайки някои прогресии за това. Тогава делението, подобно на това, се заменя с по-опростена и по-надеждна процедура - изваждане, а за да се извлече коренът на n-тата степен, е необходимо логаритъмът на радикана да се раздели на n. Решението на такава трудна задача в математиката ясно отразява целите на Напър в науката. Ето как той пише за това в началото на книгата си Рабдология:

Винаги съм се опитвала, доколкото моите способности и способности позволяват, да освободя хората от трудностите и скуката на изчисленията, досадата на която обикновено плаши много хора далеч от изучаването на математика.

Името на логаритъма е предложено от самия Напиер, което е получено чрез комбиниране на гръцки думи, които в комбинация означават „брой отношения“.

Основата на логаритъма е въведена от Спадел. Той заимствал Ойлер от теорията на степените и се прехвърлил към теорията на логаритмите. Концепцията за логаритмизма стана известна благодарение на Коп през 19 век. А използването на естествени и десетични логаритми, както и техните обозначения, се появиха благодарение на Коши.

През 1614 г. Джон Нейпиър публикува на латински есе "Описание на удивителна таблица с логаритми". Имаше кратко описание на логаритмите, правилата и техните свойства. Така че терминът "логаритъм" е установен в точните науки.

Операцията на логаритъма и първото споменаване на нея се появиха благодарение на Уолис и Йохан Бернули и най-накрая бе създадена от Ойлер през XVIII век.

Заслугата на Ойлер е да разшири логаритмичната функция на формата y = log _a x към сложната област. През първата половина на XVIII век е публикувана книгата му "Въведение в анализа на безкрайността", в която са представени съвременни дефиниции на експоненциални и логаритмични функции.

Логаритмична функция

(имеет смысл, только если: а > 0, а ≠ 1). Функция от формата y = log _a x (има смисъл само ако: a> 0 и) 1).

• Логаритмичната функция се определя от множеството от всички положителни числа, тъй като записът log _a x съществува само при условие - x> 0;
• Тази функция може да поеме абсолютно всички стойности от множеството R (реални числа). Тъй като всяко реално число b има положително x, за да удовлетвори равенството log _a x = b, това уравнение има корен - x = a ^b (следва от факта, че log _a a ^b = b).
• Функцията се увеличава на интервала а> 0 и намалява на интервала 0 <a <1.
• Ако a> 0, тогава функцията приема положителни стойности за x> 1.

Трябва да се помни, че всички графики на логаритмичната функция y = log _и x имат една стационарна точка (1; 0), тъй като log _и 1 = 0. Това ясно се вижда в илюстрацията на графиката по-долу.

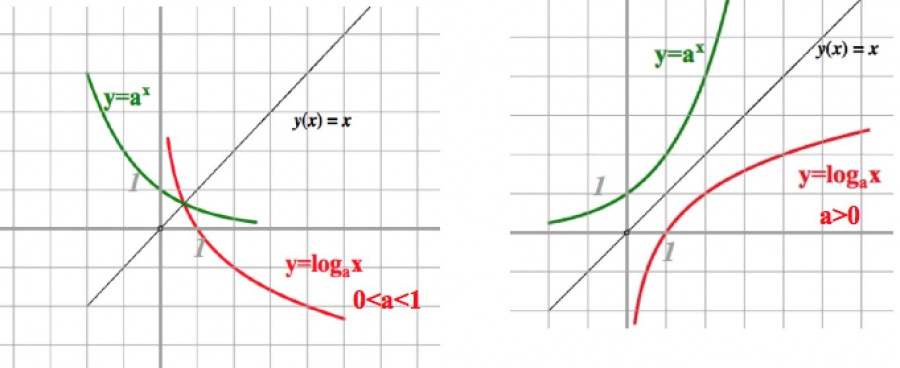
Както виждаме на снимките, функцията няма равномерност или странност, няма най-големи или най-малки стойности, не е ограничена от горе или отдолу.

Логаритмичната функция y = log _a x и експоненциалната функция y = a ^x , където (a> 0 и) 1) са взаимно обратни. Това може да се види в образа на техните графики.

Решаване на проблеми с логаритми

Обикновено решението на проблем, съдържащ логаритми, се основава на превръщането им в стандартна форма или е насочено към опростяване на изразите под знака на логаритъма. Или е необходимо да се преведат обичайните естествени числа в логаритми с необходимата основа, за да се извършат допълнителни операции за опростяване на израза.

Има някои тънкости, които не трябва да се забравят:

• При решаването на неравенствата, когато двете части стоят под логаритми според правилото с една база, не бързайте да „отхвърлите“ логаритмичния знак. Запомнете монотонните интервали на логаритмичната функция. Тъй като ако основата е по-голяма от 1 (случаят, когато функцията се увеличава) - знакът на неравенството остава непроменен, но когато основата е по-голяма от 0 и по-малка от 1 (случаят, когато функцията намалява) - знакът на неравенството се променя в обратното;
• _а х = b, а>0, а≠1 и х>0, чтобы не потерять корней из-за неучтенной области допустимых значений. Не забравяйте дефиницията на логаритъма: log _и x = b, a> 0, and 1 и x> 0, за да не загубите корените си поради нерегистрирания диапазон от валидни стойности. TLD (допустим диапазон на стойността) съществува за почти всички сложни функции.

При решаване на логаритмични уравнения се препоръчва да се използват еквивалентни трансформации. Също така трябва да внимавате и да вземете предвид възможните трансформации, които могат да доведат до загуба на някои корени.

Това са обичайни, но мащабни грешки, които много от тях са срещнали при търсенето на правилния отговор на задачата. Не са толкова много правила за решаване на логаритми, така че тази тема е по-проста от другите и следващите, но трябва да бъде добре разбрана.

заключение

Тази тема на пръв поглед може да изглежда сложна и тромава, но като я изследваш все по-дълбоко и по-дълбоко, започваш да разбираш, че темата просто свършва и трудностите не предизвикват нищо. Разгледахме всички свойства, правила и дори грешки, свързани с темата на логаритмите. Успехи в ученето!