Изобаричен процес, свързани уравнения и извличане на формулата на работата

Изобаричният процес (наричан още изобарен процес) е един от термодинамичните процеси, които протичат при индикатор за постоянно налягане. Масата на газовата система също остава постоянна. Визуалното представяне на графиката, показваща изобарния процес, се осигурява от термодинамичната диаграма в съответната координатна система.

примери

Най-простият пример за изобарен процес е нагряването на определен обем вода в отворен съд. Като друг пример може да се даде разширение на идеален газ в цилиндричен обем, където буталото има свободен ход. Във всеки от тези случаи налягането ще бъде постоянно. Тя е равна на обикновеното атмосферно налягане, което е очевидно.

реверсивност

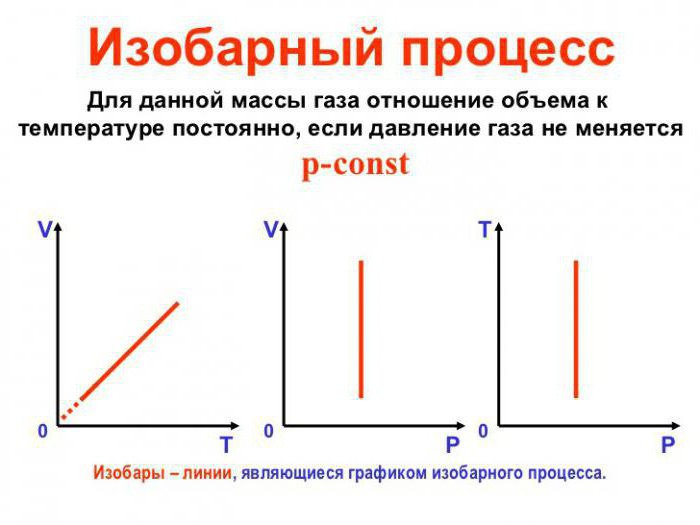
Изобаричният процес може да се приеме за обратим, ако налягането в системата съвпада с външното налягане и е равномерно във всички точки на времето на процеса (т.е. е постоянно по стойност) и температурата се променя много бавно. По този начин термодинамичното равновесие в системата се поддържа във всеки момент от времето. Това е комбинацията от горните фактори, която ни дава възможност да считаме изобарния процес за обратим.

За да се осъществи изобарен процес в системата, топлината към нея трябва или да бъде доставена или отстранена. В същото време, топлината трябва да се изразходва за работата по разширяването на идеален газ и промяната му. вътрешна енергия. Формулата, демонстрираща зависимостта на количествата един от друг по време на изобаричния процес, се нарича законът Gay-Lussac. Той показва, че обемът е пропорционален на температурата. Да изведем тази формула, основана на повърхностни знания.

Сключване на Закона за Гей-Люсак (първоначално разбиране)

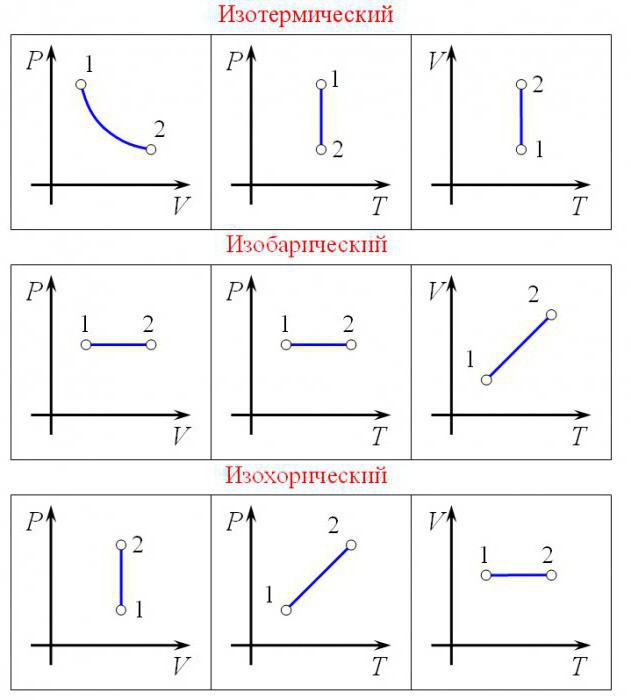
Човек, поне малко запознат с молекулярната физика, знае, че много задачи са свързани с определени параметри. Името им е налягането на газа, обема на газа и температурата на газа. В някои случаи, молекулярно и моларна маса количество на веществото, универсална газова константа и други показатели. И има определена връзка. Да поговорим по-подробно за универсалната газова константа. В случай, че някой не знае как да го получи.

Получаване на универсална газова константа

Тази константа (константно число с определено измерение) също се нарича постоянна Менделеев. Също така присъства в уравнението на Менделеев-Клапейрон за идеален газ. Как нашият известен физик получи тази константа?

Както знаем, уравнението за идеален газ има следната форма: PV / T (което звучи така: „продукт на налягане и обем, разделен на температура“). По отношение на универсалната газова константа, т. Нар Законът на Авогадро. Той казва, че ако вземем някакъв газ, тогава неговият равен брой молове при същата температура и същото налягане ще заемат същия обем.

Всъщност, това е вербалната формулировка на уравнението на състоянието за идеален газ, която е написана под формата на формула малко по-рано. Ако вземем нормалните условия (а това е, когато температурата на газа е 273,15 Келвина, налягането е 1 атмосфера, съответно, 101325 паскала, а обемът на един мол от газ е 22,4 литра) и ние ги заместваме в уравнението, умножаваме и разделяме всичко, тогава получаваме че комбинацията от такива действия ни дава цифра, равна на 8.31. Размерът е даден в джаули, разделени от произведението на мол до Келвин (j / mol * k).

Уравнение на Менделеев-Клапейрон

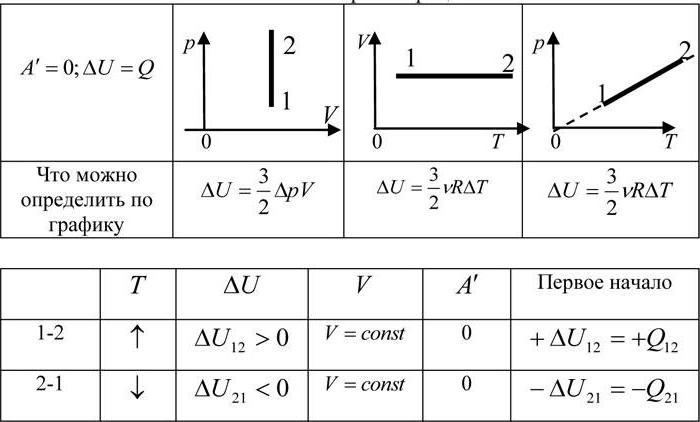
Да вземем уравнението на състоянието на идеалния газ и да го пренапишем в нова форма. Първоначалното уравнение, напомняме, има формата PV / T = R. И сега ние умножаваме двете части с температурния индекс. Получаваме формулата PV (m) = RT. Тоест продуктът на налягането по обем е равен на произведението на универсалната газова константа от температурата.

Сега умножете двете страни на уравнението с един или друг брой бенки. Ние обозначаваме техния брой с буква, да речем, X. Така получаваме следната формула: PV (m) X = XRT. Но знаем, че произведението на V с индекса "m" дава резултат само на обема V, а броят на моловете X се разкрива под формата на разделяне на конкретната маса от молната маса, т.е. тя има формата m / M.

Така, последната формула ще изглежда така: PV = MRT / m. Това е самото уравнение на Менделеев-Клапейрон, към което двамата физици са пристигнали почти едновременно. Можем да умножим дясната страна на уравнението (и в същото време да я разделим) с Номер на Авогадро. Тогава получаваме: PV = XN (a) RT / N (a). Но произведението на броя на моловете по числото на Авогадро, т.е. XN (a), ни дава нищо повече от общия брой на молекулите на газа, обозначени с буквата N.

В същото време частното на универсалната газова константа и числото на Авогадро - R / N (a) ще даде константата на Болцман (означена с k). В резултат на това получаваме друга формула, но в малко по-различна форма. Ето го: PV = NkT. Можете да отворите тази формула и да получите следния резултат: NkT / V = ​​P.

Работа с газ в изобарния процес

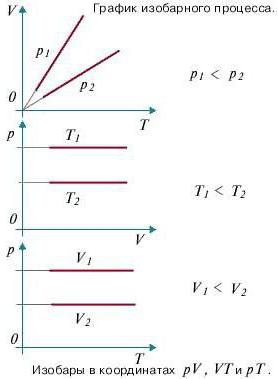
Както разбрахме по-рано, изобарният процес е термодинамичен процес, при който налягането остава постоянно. И за да разберем как ще се определи работата по време на изобаричния процес, ще трябва да се обърнем към първия закон на термодинамиката. Общата формула е следната: dQ = dU + dA, където dQ е количеството топлина, dU е промяната във вътрешната енергия, а dA е работата, извършена по време на термодинамичния процес.

Сега разгледайте конкретно изобарния процес. Вземете предвид фактора, че налягането остава постоянно. Сега се опитайте да пренапишете първия старт на термодинамиката за изобарния процес: dQ = dU + pdV. За да получите визуално представяне на процеса и работата, трябва да го изобразите в координатна система. Оста на абсцисата да е p, ординатата ос V. Да се ​​увеличи обемът. В две точки, различни една от друга със съответната стойност на р (разбира се, фиксирана), имайте предвид състоянията, представящи V1 (първоначален обем) и V2 (краен обем). В този случай графиката ще бъде права линия, успоредна на оста х.

Намирането на работа е по-лесно от всякога. Тя ще бъде просто областта на фигурата, ограничена от двете страни с издатини върху оста на абсцисата, а от третата страна - права линия, свързваща точките, съответно, в началото и в края на изобарната права линия. Нека се опитаме да изчислим стойността на работата, използвайки интеграла.

Тя ще бъде изчислена по следния начин: A = p (интеграл между V1 и V2) dV. Ние отваряме интеграла. Получаваме, че работата ще бъде равна на произведението от натиска върху разликата в обемите. Това означава, че формулата ще изглежда така: A = p (V2 - V1). Ако разкрием някои количества, ще получим друга формула. Това изглежда така: A = xR (T2 - T2), където x е количеството на веществото.

Универсална газова константа и нейното значение

Може да се каже, че последният израз ще определи физическия смисъл на R - универсалната газова константа. За да стане по-ясно, нека се обърнем към конкретни числа. Вземете за тестване един мол от вещество. В същото време, нека температурната разлика да е 1 Келвин. В този случай е лесно да се види, че газовата операция ще бъде равна на универсалната газова константа (или обратно).

заключение

Този факт може да бъде представен в малко по-различна светлина, като се формулира формулировката. Например, универсалната газова константа ще бъде числено равна на работата, извършена по време на изобарното разширение с един мол идеален газ, ако се нагрява с един келвин. Ще бъде малко по-трудно да се изчисли работата с други изопроцеси, но най-важното е да се приложи логика. Тогава всичко бързо ще падне на мястото си, а извличането на формулата ще бъде по-лесно, отколкото си мислите.