Как да намерим височината на трапеца: формула за всички поводи
Има няколко отговора на простия въпрос “Как да намерим височината на трапеца?”, Всички защото могат да се дадат различни начални стойности. Следователно, формулите ще варират.
Тези формули могат да бъдат запомнени, но те лесно се извличат. Необходимо е само да се приложат предварително изучените теореми.
Приема се във формулите
Във всички математически записи по-долу такива четения на букви са правилни.
| произволен трапец | равнобедрен трапец | името |
| и | и | долна основа |
| в | в | горната база |
| c, d | с | страни |
| п | п | височината |
| m | m | средна линия |
| d 1 d 2 | d 1 | диагонално |
| ите | ите | област |
| α, β | α | долни ъгли на дъното |
| γ, δ | γ, δ | ъгли в пресечната точка на диагоналите |
В изходните данни: всички страни
За да намерите височината на трапеца в общия случай, трябва да използвате следната формула:
n = √ (c 2 - ((a - c) 2 + c 2 - d 2 ) / (2 (a - c))) 2 ). Номер 1.
Не е най-краткият, но е доста рядък в задачите. Обикновено можете да използвате други данни.
Формулата, която ви казва как да намерите височината на равнобедрен трапец в същата ситуация е много по-кратък:
n = √ (с2 - (а - с) 2/4). Номер 2
В задачата са дадени: страни и ъгли в долната основа
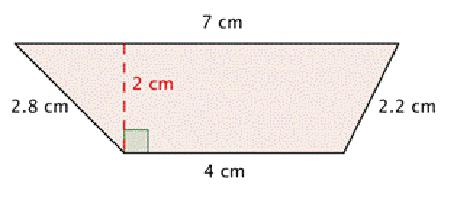
Предполага се, че ъгълът а е съседен на страната с означението "с", съответно, ъгълът β към страната d. Тогава формулата за това как да се намери височината на трапеца като цяло ще бъде:
n = c * sin α = d * sin β. Номер 3
Ако цифрата е равнобедрена, можете да използвате тази опция:
n = c * sin α = ((a - c) / 2) * tg α. Номер 4
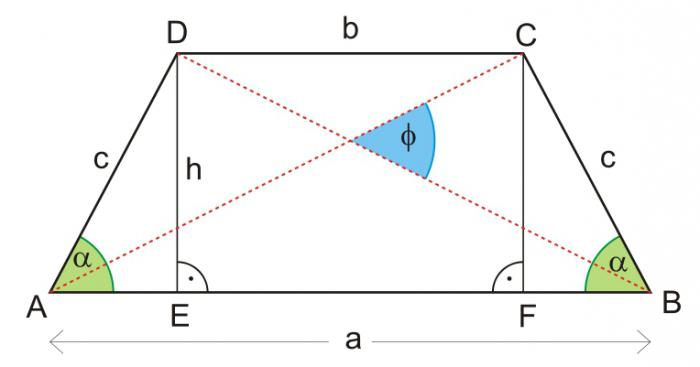
Известни: диагонали и ъгли между тях
Обикновено тези данни се свързват с все още известни стойности. Например основната или средната линия. Ако са дадени основанията, тогава отговорът на въпроса как да се намери височината на трапеца е полезен в следната формула:
n = (d 1 * d 2 * sin γ) / (a + b) или n = (d 1 * d 2 * sin δ) / (a + b). Номер 5.
Това е за цялостния вид на фигурата. Ако е даден изослоен, записът ще бъде трансформиран, както следва:
n = (d 1 2 * sin γ) / (a + b) или n = (d 1 2 * sin δ) / (a + b). Номер 6.
Когато проблемът се отнася до централната линия на трапеца, формулите за намиране на височината му стават както следва:
n = (d 1 * d 2 * sin γ) / 2m или n = (d 1 * d 2 * sin δ) / 2m. Стая 5а.
n = (d 1 2 * sin γ) / 2m или n = (d 1 2 * sin δ) / 2m. Номер 6а.
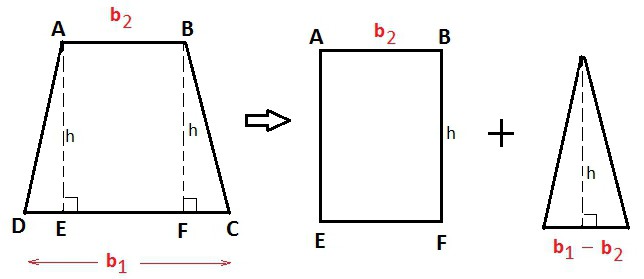
Сред известните стойности: площ с бази или средна линия
Това са може би най-кратките и най-прости формули за това как да се намери височината на трапеца. За произволна форма тя ще бъде:
n = 2S / (a + c). Номер 7.
Същото е, но с добре позната средна линия:
n = s / m. Стая 7а.
Странно, но за равнобедрен трапец, формулите ще изглеждат еднакво.
задачи
№1. От дефиницията на ъгли в долната част на трапеца.
Състояние. Дава се равнобедрен трапец, чиято страна е 5 см. Основите му са 6 и 12 см. Необходимо е да се намери синуса на остър ъгъл.
Решението. За удобство трябва да въведете нотацията. Нека долният ляв връх е A, всички останали по часовниковата стрелка: B, C, D. По този начин долната база ще бъде маркирана като АД, горната база ще бъде БЦ.
Необходимо е да се начертаят височини от върховете B и C. Точките, които показват краищата на височините, ще бъдат обозначени съответно като H1 и H2. Тъй като във фигурата BCH 1 H 2 всички ъгли са прави, това е правоъгълник. Това означава, че сегментът H1H2 е 6 cm.
Сега трябва да разгледаме два триъгълника. Те са равни, защото са правоъгълни с идентични хипотенузи и вертикални крака. Следователно по-малките им крака са равни. Следователно те могат да бъдат определени като коефициент на разликата. Последното се получава чрез изваждане от долната основа на горната. Тя ще бъде разделена на 2. Това означава, че 12 - 6 трябва да се раздели на 2. AN 1 = H 2 D = 3 (cm).
Сега от Питагоровата теорема трябва да намериш височината на трапеца. Необходимо е да се намери синуса на ъгъла. BH 1 = √ (5 2 - 3 2 ) = 4 (cm).
Използвайки знанието за това как синусът на остър ъгъл е в правоъгълен триъгълник, можем да напишем следния израз: sin α = BH 1 / AB = 0.8.
Отговорът е. Желаният синус е 0.8.
№2. Да се намери височината на трапеца от известната допирателна.
Състояние. За равнобедрен трапецовид, трябва да изчислите височината. Известно е, че основите му са 15 и 28 см. Тангенс Дан на остър ъгъл: 11/13.
Решението. Обозначението на върховете е същото като при предишната задача. Отново трябва да държите две височини от горните ъгли. По аналогия с решението на първия проблем, трябва да намерим AH 1 = H 2 D, които се дефинират като разлика 28 и 15, разделени на две. След изчисленията се оказва, че: 6.5 cm.
Тъй като допирателната е съотношението на два крака, можем да напишем следното равенство: tg α = AH 1 / BH 1 . Освен това това съотношение е 11/13 (по условие). Тъй като AN 1 е известен, е възможно да се изчисли височината: VN 1 = (11 * 6.5) / 13. Простите изчисления дават резултат от 5.5 cm.
Отговорът е. Необходимата височина е 5,5 cm.
№3. За изчисляване на височината на известните диагонали.
Състояние. За трапец е известно, че диагоналите му са 13 и 3 см. Необходимо е да се знае височината му, ако сумата на основите е 14 см.
Решението. Нека обозначението на фигурата е същото, както преди. Да предположим, че говорителят е по-малък диагонал. От върха C трябва да задържите желаната височина и да го обозначите като CH.
Сега трябва да извършите допълнително строителство. От ъгъла C, трябва да начертаете права линия, успоредна на по-големия диагонал и да намерите точката на пресичането му с продължаването на страната на кръвното налягане. Това ще бъде D 1 . Оказа се нов трапецовид, в който е изчертан триъгълникът ASD 1 . Това е необходимо и за по-нататъшното решаване на проблема.
Желаната височина също ще бъде в триъгълника. Следователно, можете да използвате формули, изучени в друга тема. Височината на триъгълника се определя като произведение на числото 2 и площта, разделена от страната, на която е изтеглена. А страната е равна на сумата от основите на първоначалния трапец. Това се основава на правилото, че допълнителното строителство е извършено.
В разглеждания триъгълник са известни всички страни. За удобство въвеждаме обозначението x = 3 cm, y = 13 cm, z = 14 cm.
Сега можете да преброите района, като използвате теоремата на Герона. Полу-периметърът ще бъде p = (x + y + z) / 2 = (3 + 13 + 14) / 2 = 15 (cm). Тогава формулата за областта след заместването на стойностите ще изглежда така: S = √ (15 * (15 - 3) * (15 - 13) * (15 - 14)) = 6 √ 10 (cm 2 ).
Сега трябва да преброите височината: n = (2 * 6 )10) / 14 = 6 /10 / 7 (cm).
Отговорът е. Височината е 6√10 / 7 cm.
№4. Да търсим височини от двете страни.
Състояние. Дава се трапецовидност, трите страни на която са 10 см, а четвъртата 24 см. Трябва да знаете височината му.
Решението. Тъй като фигурата е равнобедрена, тогава ще ви е нужна формула номер 2. В нея просто трябва да замените всички стойности и да преброите. Тя ще изглежда така:
n = √ (10 2 - (10 - 24) 2/4) = (51 (cm).
Отговорът е. п = 50 cm