Експониране: Основна математика в програмирането

Често се сблъскваме с факта, че трябва да повишим броя до всяка степен. Можете да използвате обичайния калкулатор. Но това не е интересно и много често не отговаря на условията на задачата.

Понятие за степен по математика

Тя трябва да започне с обяснение на математическия смисъл на експоненцирането. Например, ние трябва да повишим някакъв брой x до силата на y. В математиката този запис би изглеждал така: x ^y = x ^ y. Това означава, че броят x трябва да се умножи сам по себе си y пъти. Не забравяйте: каквото и число да изградите до нулевата степен, получавате едно и когато изграждате първата сила, получаваме оригиналния номер. При конструирането на отрицателна степен ние просто превръщаме резултата.

Експониране в паскал

С математиката всичко е ясно. Но как да направим такава програма, която ще доведе до експоненциализиране? Това е просто. Ако трябва да повишим x до силата на 5, тогава нашият код ще изглежда така: res: = x * x * x * x * x. Умножихме числото с 5 пъти, както ни беше необходимо, но какво да правим, ако не знаем до каква степен трябва да се повиши броят? След това ще разгледаме как да се направи експоненция. Паскал не ни дава много възможности за това, но ние определено ще измислим нещо. Например, като се използват стандартни функции и процедури или се използват различни цикли.

Квадратиране на номер

Да започнем с изграждането на площад. Квадратирането е специален случай на експониране. За да направите това, pascal предоставя стандартната процедура sqr (x). Тя ще повиши нашия номер x в квадрата, този запис е равен на записа x * x.

Много често това е съвсем достатъчно, но не винаги програмата може да бъде ограничена до само едно квадратче. Как да изградим по-висока степен? Прочетете за него и обучете.

Използване на стандартни оператори

В Паскал има два метода за повишаване на число до сила: exp (ln (x) * y) и метод на мощност (x, y). Процедурата exp () има ограничение: x трябва да е по-голямо от 0, тъй като невъзможно е да се извлече естественият логаритъм от непозитивен номер, но тази функция се счита за остаряла и неудобна за използване, затова няма да говорим повече за нея. Функцията power () отнема две стойности, като първото число (x) се повишава до мощност, второто число (y) до мощността, която трябва да се повиши и връща x на силата на y. Трябва да се помни, че числата x и y са реални, т.е.

Но има един недостатък, тази функция не е във всички версии на Pascal. Както и да е, понякога експоненцията трябва да се извършва без използването на оператори. Продължете и разглобете следния метод.

Експониране с цикъл for

Както вече разбрахме, повишаването на числото на власт е последователно умножение на число само по себе си няколко пъти. Повтарянето на действие няколко пъти в програмирането е много по-лесно, отколкото в живота. Използвайте цикъла for:

Ще разберем какво и как работи тук. Първо, въвеждаме две числа: x и y. Тогава ще вземем единицата за резултата, за който тя е - по-долу. Извършете цикъл до модула на нашата степен, тъй като ако степента е отрицателна, цикълът няма да продължи. В цикъла, умножаваме резултата си със самото число х. Защо тогава присвояваме резултата на 1? Първо, ако се умножи по 0, тогава програмата винаги ще даде 0. На второ място, нашата степен може да бъде равна на 0, тогава програмата трябва да ни върне 1, защото всеки брой в 0 градуса е 1. След това проверяваме дали степента е отрицателна или положителна: ако е отрицателна, тогава разделяме единицата на нашия резултат. Изпълнението на тази задача с цикъл while се извършва по същия начин.

Използване на цикъл while в експоненциране

Използването на цикъл while е по-правилно, отколкото за, но предишната версия е по-лесна за разбиране. Едва ли е възможно да се ограничим само до един за цикъл, за разбирането би било по-добре да погледнем няколко примера, а задачата е зададена по различен начин, за някой с един цикъл, за някой друг, затова ще анализираме друг метод на експоненциране.

Всичко е почти същото както преди. Въведете две числа x и y. Ние присвояваме единичната стойност на нашия резултат, за да се повишим до нулева степен. След това създаваме брояч i и му присвояваме стойността на модула. Цикълът продължава, докато броячът е нула, ако степента е нула от самото начало, цикълът няма да бъде изпълнен, резултатът ще остане такъв, какъвто би трябвало да бъде, защото всяко число в нулевата степен е едно. В самия цикъл ние все още разглеждаме резултата, като умножаваме резултата вече получен с нашето число х, не забравяме да извадим един от нашия брояч, в противен случай никога няма да достигнем нула. Ами тогава, точно както по-горе, конверсията, ако степента е отрицателна. Нищо сложно, както се оказа. Но никой не се съмняваше.

Е, накрая сме с обикновени числа, но има не само такива числа.

Концепцията за комплексните числа

От самото начало на училищното образование ни се обясняват само обикновени номера, но има и други, например сложни числа. Те са доста трудно да си представим, особено като се има предвид факта, че почти никога не сме запознати с тях. В математическата нотация те имат формата z = x + yi, където x и y са някои числа, а i е ментална единица. Вие веднага си помислили: това е често срещано число, просто трябва да извършите операцията по добавяне. Но не, не толкова просто. Това не е сума, а число. С други думи, ако се опитате да представите всичко това от гледна точка на геометрията, тогава можете да замените знака на добавянето с точка и запетая и да получите координатите на точката, x и y. И ако изградим нулев вектор до тази точка, тогава можем визуално да видим всичко това. Изглежда, че текстът е станал твърде много, да видим малко:

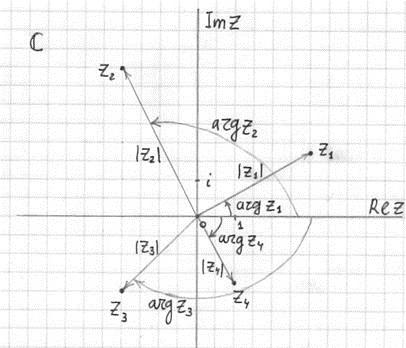
Ако искаме да покажем, че нашата равнина е сложна, достатъчно е да я отбележим с получер шрифт С, като този. Тогава можем да видим много точки, да ги разгледаме и да се опитаме да разберем кой от тях е записан. Вземете точката z _1, снижете проекцията на оста ReZ и вземете 3, след това върху оста lmZ и вземете 1.75, в резултат на което имаме числото z ₁ = 3 + 1.75i. Изглежда всичко е ясно, нека отново да се консолидираме. Точка z ₂ , на хоризонталната ос - две, на вертикалната - четири, в резултат на това имаме: z ₂ = 2 + 4i. Всичко е много ясно и просто.

При комплексните числа са възможни същите операции както при обикновените. Добавяне, изваждане, умножение, деление. Но в тази статия ще се съсредоточим върху изграждането на комплексно число към властта.

Повишаване на силата на комплексно число

Какво да направя, ако трябва да се изгради сложен номер? Не се паникьосвайте! Всичко е точно като с обикновените числа, но малко по-сложно. Да започнем с квадрата. Като се има предвид броят z = 2 + 5i. Ние квадрат, получаваме z ² = (2 + 5i) ² = (2 + 5i) (2 + 5i) - и това е обичайното двучленно, можете просто да умножите, да дадете подобни термини и всичко. Много е просто, но какво да правя, когато трябва да се изгради в по-висока степен? Първо, номерът ни трябва да бъде представен в тригонометрична форма, например:

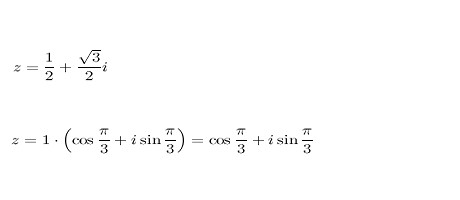
Тогава е необходимо да се използва формулата за конструиране на комплексни числа в тригонометричната форма: z ⁿ = | z | ⁿ * (cos (nx) + i * sin (nx)). Може да се отбележи, че при изграждането на комплексни числа, дори в много голяма степен, те не се променят много, така че не се притеснявайте, че е трудно, но с практиката всичко ще дойде.

По този начин, сега знаете как да повишите цифрите до власт в математиката, в езика за програмиране Паскал, вие също научихте какво са сложни числа и как да ги изградите до сила. Всичко се оказа много по-просто, отколкото си мислехте. Не е ли? Остава само да се опита всичко на собствения си опит, и всичко ще падне на мястото си. Всяка задача, свързана с експоненцирането, сега е решена много лесно за вас.