Равновесно състояние на лоста. Правилото на моментите. Прости механизми. Задачи и решения
От незапомнени времена човечеството е използвало различни механизми, които са предназначени да улесняват физическия труд. Един от тях е лост. Какво е това, каква е идеята за нейното използване и какво е условието за равновесие на лоста, тази статия е посветена на разглеждане на всички тези въпроси.
Кога човечеството започна да прилага принципа на лоста?

Трудно е да се отговори точно на този въпрос, тъй като древните египтяни и жителите на Месопотамия вече познаваха прости механизми още три хиляди години преди новата ера.
Един от тези механизми е така нареченият лост-кран. Той представляваше дълъг полюс, който се намираше на опората. Последният е инсталиран по-близо до единия край на стълба. Към края, който беше по-далеч от референтната точка, те завързаха кораб, а от другата поставиха някакъв противотежест, например камък. Системата се регулира по такъв начин, че напълнен наполовина съд води до хоризонталното положение на полюса.
Ad
Крановият лост служи за повдигане на вода от кладенец, река или друга депресия до нивото на лицето. Чрез прилагане на малка сила към съда, човекът я спусна към водоизточника, съдът се напълни с течност и след това, прилагайки малка сила към другия край на стълба с противотежест, е възможно да се повдигне посоченият съд.
Легендата за Архимед и кораба
Всеки знае древногръцкия философ от град Сиракуза, Архимед, който в своите писания не само описва принципа на действие на простите механизми (лост, наклонена дъска), но и води до съответните математически формули. До ден днешен фразата му остава известна:
Дай ми опора и аз ще премести този свят!

Както знаете, никой не му е давал такава подкрепа и Земята остава на мястото си. Но това, което Архимед наистина можеше да се движи, беше корабът. Една от легендите на Плутарх (творбата "Паралелни животи") казва следното: Архимед, в писмо до своя приятел, цар Хиерон от Сиракуза, каза, че сам може да премести произволно голямо тегло при определени условия. Хиерон беше изненадан от подобно изявление от философа и го помоли да покаже за какво говори. Архимед се съгласи. На един от дните корабът на Хиерон, на пристана, беше натоварен с хора и бъчви, пълни с вода. Философът, седнал на разстояние от кораба, успял да го вдигне над водата, дърпайки въжетата, като прилагал малко усилия.
Компоненти на лоста
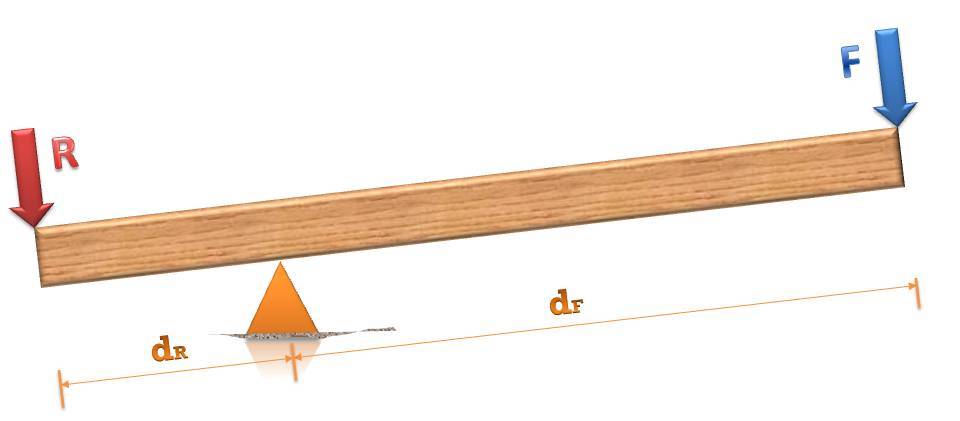
Въпреки факта, че говорим за доста прост механизъм, той все още има определено устройство. Физически, тя се състои от две основни части: стълб или греда и опора. При разглеждането на същите задачи, полюсът се разглежда като обект, състоящ се от две (или една) рамена. Рамото е част от полюса, която е по отношение на опората от едната страна. Голяма роля в принципа на действие на разглеждания механизъм има точно дължината на рамото.
Когато разглеждаме лоста в работата, има два допълнителни елемента: приложената сила и сила за противодействие. Първият се опитва да задвижи обект, който създава сила на опозицията.
Ad
Равновесно състояние на лоста във физиката
Запознати с устройството на този механизъм, ние представяме математическа формула, с която можем да кажем коя ръка на лоста ще се движи в посоката или, обратно, цялото устройство ще бъде в покой. Формулата е във формата:
F 1 * l 1 = F 2 * 1 2 ,
където F 1 и F 2 са силите на действие и реакция, съответно, l 1 и l 2 са дължините на рамената, към които се прилагат тези сили.
Този израз ви позволява да изследвате условията на равновесие на лост, който има ос на въртене. Така че, ако рамото l1 е по-голямо от l2, тогава за балансиране на силата F 2 се нуждаете от по-малка стойност F 1 . Напротив, ако l 2 > l 1 , тогава, за да противодейства на силата F 2, ще трябва да прикрепите голям F1. Тези заключения могат да бъдат получени чрез пренаписване на израза по-горе в следната форма:
Ad
F 1 / F 2 = l 2/1 1 .
Както може да се види, силите, участващи в процеса на формиране на равновесие, са обратно пропорционални на дължината на рамената на лоста.
Каква е печалбата и загубата при използване на лоста?
Важно заключение следва от горните формули: с помощта на дълга ръка и малко усилие могат да бъдат преместени обекти с огромна маса. Това е вярно и мнозина могат да мислят, че използването на лост води до печалба в работата. Но това не е така. Работата е количество енергия, което не може да бъде създадено от нищо.
Нека анализираме работата на обикновен лост с две втвърдяване l 1 и l 2 . Да предположим, че в края на рамото L2 има тегло на тежестта Р (F2 = Р). В края на другото рамо лицето прилага силата F 1 и повишава този товар до височината h. Сега, да изчислим работата на всяка сила и да приравним получените резултати. Получаваме:
Ad
F 1 x = F 2 * h.
Силата F 2 действаше по вертикална траектория с дължина h, на свой ред F1 действаше и по вертикала, но вече беше прикрепена към другата ръка, чийто край се движи с неизвестна величина x. За да го намерим, е необходимо в последния израз да се замени формулата на връзката между силите и ръцете на лоста. Като изразяваме x, имаме:
x = F 2 * h / F 1 = l 1 * h / l 2 .
Това равенство показва, ако l 1 > l 2 , тогава F 2 > F 1 и x> h, т.е. прилагайки малка сила, можете да повдигнете товар с голямо тегло, но трябва да преместите съответния лост (l 1 ) към по-голям. разстоянието. Напротив, ако l 1 <l 2 , тогава F 2 <F 1 и x <h, т.е. теглото на определено тегло може да се повиши до по-голяма височина h чрез преместване на рамото l1 до по-малка амплитуда, но трябва да се приложи достатъчно голяма сила F 1 , В първия случай се получава усилването на мощността, във втория по начин или скорост.
По този начин лостът не се ползва от работа, той позволява само да се преразпределя или в полза на по-малка приложена сила, или в полза на по-голяма амплитуда на движение на обекта. Общият философски принцип работи в обсъжданата физика: всяка печалба се компенсира от определена загуба.
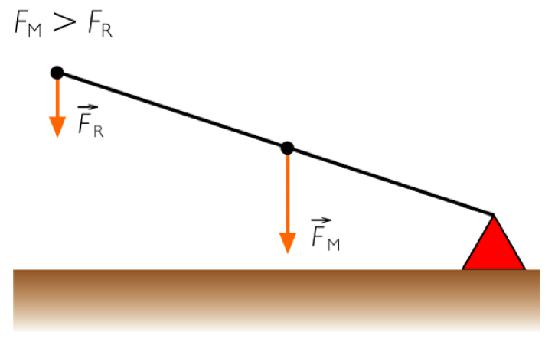
Видове лостове
В зависимост от силата на прилагане и позицията на опората се разграничават следните видове:
- Първият вид: опората е между двете сили F 1 и F 2 , следователно дължината на ръцете ще определи какво дава такова предимство. Пример за това са обикновени ножици.
- Вторият вид. Тук силата, срещу която се извършва работата, се намира между подкрепата и приложената сила. Този вид конструкция означава, че той винаги ще дава сила и загуба на пътуване и скорост. Неговият пример е градинска кола.
- Третият вид. Последната опция, която остава да се реализира в тази проста конструкция, е позицията на приложената сила между опората и силата на съпротивлението. В този случай, печалбата по пътя, но загубата е в сила. Пример за това са пинсети.

Концепцията за момента на силата
Разглеждането на всякакви проблеми в механиката, които включват понятията ос или точка на въртене, се извършва с помощта на правилото за момент на силата. Тъй като опората на лоста е и оста (точка), около която системата се върти, моментът на сила също се използва за оценка на равновесието на този механизъм. С това се има предвид количество във физиката, равно на произведението на рамото и действащата сила, а именно:
M = l * F.
Като се има предвид това определение, състоянието на лостовото равновесие може да бъде пренаписано, както следва:
M 1 = M 2 , където M 1 = l 1 * F 1 и M 2 = l 2 * F 2 .
Моментът М е адитивен, което означава, че общият момент на сила за въпросната система може да се получи чрез обичайното добавяне на всички моменти, действащи върху нея. Въпреки това, трябва да се вземе под внимание техният знак (силата, която кара системата да се върти обратно на часовниковата стрелка, създава положителен момент + M, и обратно). С това казано, правилото на моментите за лост, който е в баланс, ще изглежда така:
Ad
М1-М2 = 0.
Лостът губи баланса си, когато M 1 ≠ M 2 .
Къде се използва принципът на ливъридж?
Вече споменахме някои примери за използването на този прост и добре познат механизъм от древни времена. Ето само няколко допълнителни примера:
- Клещи: лост от първи вид, който ви позволява да създавате огромни усилия поради малката дължина на раменете l 2, където се намират зъбите на инструмента.
- Капачките и бутилките на капачките за отваряне: това е лост от 2-ри вид, така че винаги печели усилието.
- Риболовен прът: лостът от 3-ти вид, който ви позволява да преместите края на въдицата с поплавък, грузило и кука за големи амплитуди. Загубата в този случай се усеща, когато рибарът намира за трудно да извади рибата от водата, дори ако теглото му не надвишава 0,5 кг.

Самият човек със ставите, мускулите, костите и сухожилията е ярък пример за система с много различни лостове.
Решаване на проблеми
Равновесното състояние на лоста, обсъден в статията, се използва за решаване на прост проблем. Необходимо е да се изчисли приблизителната дължина на рамото на лоста, прилагайки усилие, до края на което Архимед е в състояние да вдигне кораба, както го описва Плутарх.

За да решим, въвеждаме следните предположения: вземаме под внимание гръцката трирема от 90 тона с изместване и приемаме, че подкрепата на лоста е 1 метър от центъра на масата. Както Архимед, според легендата, може лесно да вдигне кораба, тогава ще приемем, че за тази цел той е приложил сила, равна на половината от теглото си, т.е. около 400 N (за маса от 82 кг). След това, прилагайки равновесното състояние на лоста, получаваме:
F 1 * l 1 = F 2 * l 2 => l 1 = F 2 * l 2 / F 1 = m * g * l 2 / F 1 = 90000 * 9,81 * 1/400 ≈ 2,2 km.
Дори ако увеличим силата, приложена към стойността на теглото на самия Архимед и прибавим опората още два пъти, тогава дължината на рамото ще бъде около 500 метра, което също е голяма стойност. Най-вероятно легендата за Плутарх е преувеличение, за да се демонстрира ефективността на лоста, а Архимед не вдигна кораба над водата.