Египетски триъгълник - мистерията на древността

Известният математик Питагор е направил много различни открития, но за повечето хора, които не трябва редовно да се занимават с алгебра и геометрия, той е известен със своята теорема. Ученият го е открил, оставайки в Египет, където е очарован от красотата и елегантността на пирамидите, а това, от своя страна, го подтиква към идеята, че определена форма може да бъде проследена в тяхната форма.

История на откриването

Египетският триъгълник дължи името си на елините, които често посещават Египет през VII-V в. Пр. Хр. например, сред тях е Питагор. основа пирамидите на Хеопс е правоъгълен многоъгълник и Пирамида на Хефре - така нареченият египетски триъгълник, който древните наричат ​​свещени. Плутарх пише, че хората на Египет корелират природата с тази геометрична фигура: вертикалният крак символизира човека, основата жената и хипотенузата на детето. Съотношението в нея е 3: 4: 5 и това води до Питагоровата теорема, тъй като 3 ² x 4 ² = 5 ² . Следователно фактът, че в основата на пирамидата на Хефр лежи египетският триъгълник, предполага, че известната теорема е била известна на жителите на древния свят преди Питагор да го формулира. Особеността на тази фигура е и фактът, че поради това съотношение, това е първият и най-простият от триъгълниците на Heron, тъй като неговите страни и област са цели числа.

приложение

Египетският триъгълник от древността е бил популярен в архитектурата и строителството.

Тя се използва главно при изграждане на прави ъгли с въже или въже, разделено на 12 части. От знаците на такова въже може много точно да се създаде правоъгълна фигура, краката на която да служат като водачи за определяне на правилния ъгъл на конструкцията. Известно е, че такива свойства на това геометрична форма не само в Древен Египет но много преди това в Китай, Вавилон и Месопотамия. Египетският триъгълник е бил използван и за създаване на пропорционални структури през Средновековието.

ъгли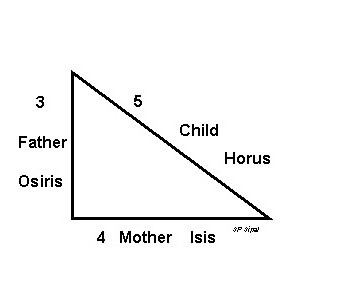

Аспектното съотношение на този триъгълник е 3: 4: 5, което води до това, че той е правоъгълен, т.е. един ъгъл е равен на 90 градуса, а другите два - 53,13 и 36,87 градуса. Ъгълът между страните е прав, а съотношението е 3: 4.

Доказателство за

Използвайки няколко прости изчисления, можем да докажем, че триъгълникът е правоъгълен. Ако следваме обратната теорема на тази, създадена от Питагор, т.е. ако сумата на квадратите на двете страни е равна на третия квадрат, тогава тя е правоъгълна, и тъй като нейните страни водят до равенство 3 ² x 4 ² = 5 ² , следователно, е правоъгълна.
Обобщавайки, трябва да се отбележи, че египетският триъгълник, чиито свойства са били известни на човечеството от векове, продължава да се използва в архитектурата днес. Това изобщо не е изненадващо, защото този метод гарантира точност, която е много важна по време на строителството. В допълнение, той е много лесен за използване, което също значително опростява процеса. Всички предимства на използването на този метод са тествани от векове и остават популярни досега.