Дискриминант: примери за решения. Как да решим квадратични уравнения чрез дискриминант
Квадратните уравнения често се появяват при решаването на различни проблеми на физиката и математиката. В тази статия ще разгледаме как да разрешим тези равенства по универсален начин "чрез дискриминант". В статията са дадени и примери за използване на придобитите знания.
Какви уравнения говорим?
Фигурата по-долу показва формула, в която x е неизвестна променлива, а латинските букви a, b, c са известни числа.
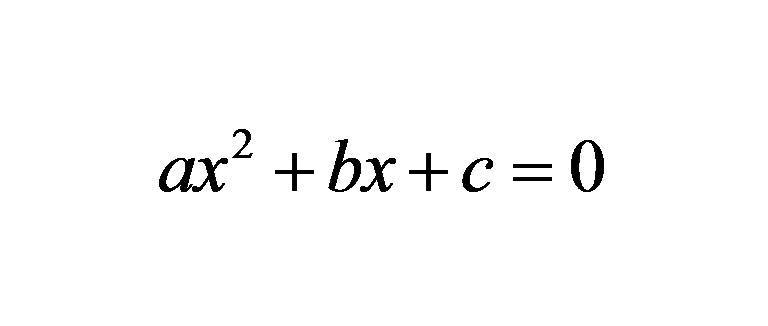
Всеки от тези символи се нарича коефициент. Както можете да видите, числото "а" стои пред променливата x на квадрат. Това е максималната степен на изразяване, така че тя се нарича квадратично уравнение. Другото му име често се използва: уравнение от втори ред. Стойността на себе си е квадратен коефициент (стоящ с променлива на квадрат), b е линеен коефициент (той е до променлива, издигната до първата сила), и накрая, числото c е свободен термин.
Забележете, че видът на уравнението, което е показано на фигурата по-горе, е обикновен класически квадратен израз. Освен това има и други уравнения от втори ред, в които коефициентите b, c могат да бъдат нула.
Ad
Когато задачата е да се реши разглежданото равенство, това означава, че трябва да се намерят такива стойности на променливата х, които биха го удовлетворили. Тук първото нещо, което трябва да направите, е да запомните следното: тъй като максималната степен на X е 2, този тип израз не може да има повече от 2 решения. Това означава, че ако при решаването на уравнението бъдат открити 2 стойности на х, които да го удовлетворят, тогава можете да сте сигурни, че няма трето число, което да замества, че вместо x, равенството също би било вярно. Уравнителните решения в математиката я наричат корени.
Начини за решаване на уравнения от втори ред
Разрешаването на уравнения от този тип изисква познаване на някои теории за тях. В училищния курс по алгебра се разглеждат 4 различни метода на решение. Ние ги изброяваме:
- използване на факторизация;
- използвайки формулата за пълния квадрат;
- прилагане на графиката на съответната квадратична функция;
- използвайки дискриминантното уравнение.
Плюс първият метод е неговата простота, но не може да се приложи за всички уравнения. Вторият метод е универсален, но донякъде тромав. Третият метод се отличава със своята яснота, но не винаги е удобен и приложим. И накрая, използването на дискриминантното уравнение е универсален и сравнително прост начин да се намерят корените на абсолютно всяко уравнение от втори ред. Затова в статията разглеждаме само него.
Формулата за получаване на корените на уравнението
Нека се обърнем към общата форма на квадратното уравнение. Записваме го: a * x² + b * x + c = 0. Преди да се използва метода за решаването му "чрез дискриминант", е необходимо да се намали равнопоставеността винаги към записаната форма. Това означава, че трябва да се състои от три термина (или по-малко, ако b или c е 0).
Ad
Например, ако има израз: x²-9 * x + 8 = -5 * x + 7 * x², тогава трябва първо да прехвърлите всичките му членове на една и съща страна на уравнението и да добавите термините, съдържащи променливата x, в равни правомощия.
В този случай, тази операция ще доведе до следния израз: -6 * x²-4 * x + 8 = 0, което е еквивалентно на уравнението 6 * x² + 4 * x-8 = 0 (тук умножаваме лявата и дясната страна на равенството с -1) ,
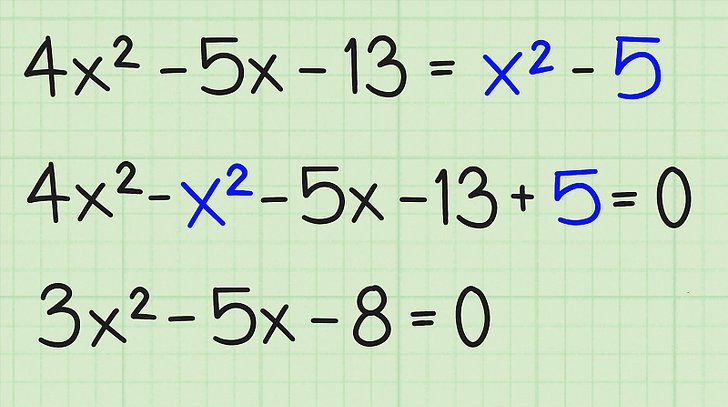
След като се научи по-горе, трябва да се научите да различавате коефициентите. Всичко тук е просто: когато x² винаги е a, когато x 1 е b, свободният член c е число, което не е свързано с x.
В горния пример a = 6, b = 4, c = -8. Отбележете, че всички членове на разглежданото равенство винаги се сумират помежду си, следователно, ако се появи знакът "-", това означава, че съответният коефициент е отрицателен, като в този случай c.
Ad
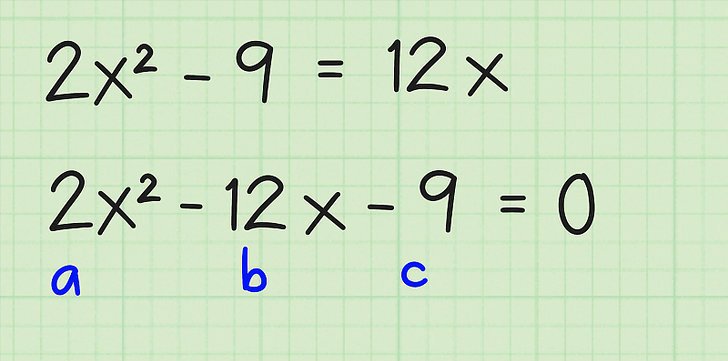
След като анализираме този момент, сега се обръщаме към самата формула, която дава възможност да се получат корените на квадратичното уравнение. Изглежда, че е показано на снимката по-долу.
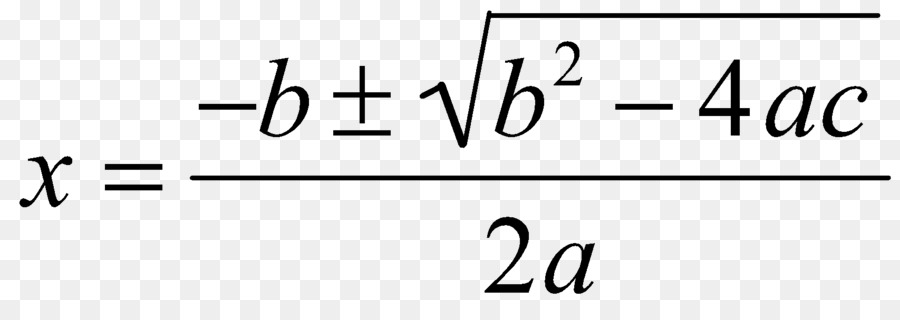
Както може да се види от този израз, той ви позволява да получите два корена (трябва да обърнете внимание на знака "±"). За да направите това, е достатъчно да замените коефициентите b, c и a.
Понятие за дискриминант
В предишния абзац беше дадена формула, която ви позволява бързо да разрешите всяко уравнение от втори ред. В него кореновата експресия се нарича дискриминант, т.е. D = b²-4 * a * c.
Защо тази част от формулата е изолирана и дори има собствено име? Факт е, че дискриминантът свързва всичките три коефициента на уравнението в един израз. Последният факт означава, че той напълно носи информация за корените, което може да бъде изразено в следния списък:
Ad
- D> 0: равенството има 2 различни решения, като и двете са реални числа.
- D <0: също се получават два корена, но и двата са сложни. Този вид изразяване е научен да се решава едва през Възраждането, когато понятието за „въображаема единица“ е въведено от математиците на новото време.
- D = 0: уравнението има само един корен и е реално число.
В статията са дадени примери за дискриминантни квадратични уравнения и тяхното решение.
Задачата за определяне на дискриминанта
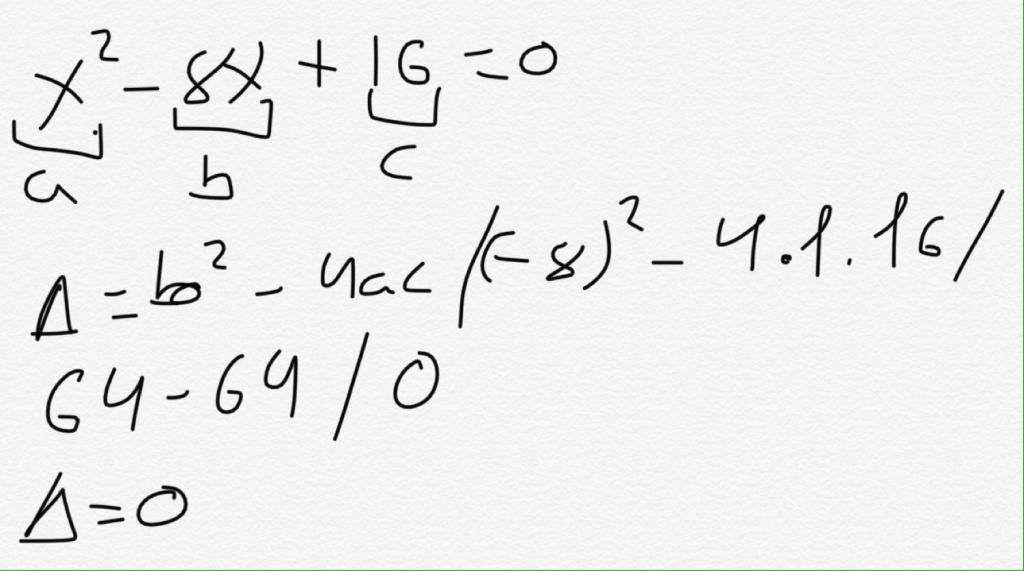
Даваме прост пример как да се намери дискриминант. Нека да се даде следното равенство: 2 * x² - 4 + 5 * x-9 * x² = 3 * x-5 * x² + 7.
Привеждаме го към стандартната форма, получаваме: (2 * x²-9 * x² + 5 * x²) + (5 * x-3 * x) + (- 4-7) = 0, откъдето стигаме до равенство: -2 * x² + 2 * x-11 = 0. Тук a = -2, b = 2, c = -11.
Сега можете да използвате формулата за дискриминант: D = 2² - 4 * (- 2) * (- 11) = -84. Полученото число е отговорът на задачата. Тъй като в примера дискриминантът е по-малък от нула, можем да кажем, че това квадратично уравнение няма реални корени. Неговото решение ще бъде само номерата на сложния тип.
Пример за неравенство чрез дискриминант
Ние решаваме задачи с малко по-различен тип: даденото равенство е -3 * x²-6 * x + c = 0. Необходимо е да се намерят стойности c, за които D> 0.
В този случай са известни само 2 от трите коефициента, следователно точната стойност на дискриминанта не може да бъде изчислена, но е известно, че тя е положителна. Последният факт се използва при конструирането на неравенството: D = (-6) ²-4 * (- 3) * c> 0 => 36 + 12 * c> 0. Решението на полученото неравенство води до резултат: c> -3.
Ad
Проверете получения номер. За да направим това, изчисляваме D за 2 случая: c = -2 и c = -4. Числото -2 удовлетворява получения резултат (-2> -3), съответният дискриминант ще има стойността: D = 12> 0. От своя страна, числото -4 не отговаря на неравенството (-4 <-3), изчисляваме дискриминанта: D = -12 <0, което противоречи на състоянието на проблема.
Така, всички числа c по-големи от -3 ще удовлетворят условието.
Пример за решаване на уравнение
Представяме проблема, който се състои не само в намирането на дискриминанта, но и в решаването на уравнението. Необходимо е да се намерят корените за равенството -2 * x² + 7-9 * x = 0.
В този пример дискриминантът е равен на следната стойност: D = 81-4 * (- 2) * 7 = 137. Тогава корените на уравнението се дефинират като: x = (9 ± √137) / (- 4). Това са точните стойности на корените, ако изчисляваме корените приблизително, тогава получаваме числата: x = -5.176 и x = 0.676.
Геометричен проблем
Ще решим проблем, който ще изисква не само способността за изчисляване на дискриминанта, но и прилагането на уменията на абстрактното мислене и знание, как да се правят квадратични уравнения.
Боб имаше одеяло с размери 5 х 4 метра. Момчето искаше да го шие по периметъра на солидна лента от красива материя. Колко дебела ще бъде тази лента, ако се знае, че Боб има 10 м² плат.

Нека лентата е с дебелина х m, след което площта на тъканта по протежение на дългата страна на одеалото ще бъде (5 + 2 * x) * x, и тъй като дългите страни са 2, имаме: 2 * x * (5 + 2 * x). На късата страна площта на пришитата тъкан ще бъде 4 * x, тъй като тези страни са 2, получаваме стойността на 8 * x. Забележете, че стойността на 2 * x е добавена към дългата страна, тъй като дължината на одеялото се увеличава с това число. Общата площ на тъканта, пришити към одеялото, е 10 m². Затова получаваме равенство: 2 * x * (5 + 2 * x) + 8 * x = 10 => 4 * x² + 18 * x-10 = 0.
За този пример дискриминантът е: D = 18²-4 * 4 * (- 10) = 484. Коренът му е 22. Използвайки формулата, намираме желаните корени: x = (-18 ± 22) / (2 * 4) = (- 5, 0,5). Очевидно от двата корена, само числото 0.5 е подходящо за състоянието на проблема.
По този начин лентата от тъкани, която Боб шие към одеялото си, ще бъде с широчина 50 cm.