Пример за алгоритъм на Дифи Хелман
Разкриването на темата за криптографията с публичен ключ трябва да започне с историческия път на проблема. Уитфийлд Дифи и Мартин Хелман бяха първите, които попитаха за отворения метод за предаване на ключове. Това се случи през 1976 година. Публикацията направи първите опити да се справи с проблема. Решението им не беше без недостатъци, но постави основата за един напълно различен начин на мислене в областта на кодирания трансфер на данни.
Предпоставки за създаване на алгоритъм Дифи-Хелман
До този момент удостоверяването и шифроването бяха възможни само чрез споделен секретен ключ. С развитието на технологиите въпросът стана по-остър. Ако 10 души трябва да прехвърлят данни помежду си по несигурни канали, ще трябва да обменят пароли помежду си. Тази задача изглежда съвсем реална. Дори и с необходимостта да ги актуализираме. В крайна сметка, за 10 приятели ще ви трябват само 45 секретни ключа. И ако контактите ще бъдат 100? Ще са необходими 4950 пароли. Ситуацията нараства като снежна топка.
Основното постижение на Дифи и Хелман беше правилното формулиране на въпроса и гениалния отговор. Те предложиха данните да бъдат криптирани по един начин и да бъдат декриптирани в друга. Това означава, че има 2 ключа. Използваният за криптиране може да бъде оставен отворен. По този начин всяко лице може да шифрова съобщение, но само собствениците на втория секретен ключ могат да го декриптират. Но как да приложим алгоритъма за прехвърлянето на такъв ключ? Учените са могли частично да дадат отговор.
Кратка математика: групи
Алгоритъмът на Diffie-Hellman или протоколът (по-нататък DH) работи с помощта на прости числа. Нека a е достатъчно голям номер, принадлежащ на множеството прости числа. Алгоритъмът включва използването на 250-500 байта. Нека Za е мултипликативната група на остатъчния пръстен по модул a, която ще бъде използвана от алгоритъма на криптиране Diffie-Hellman. Състои се от набор от числа 1, ..., a-1.
Вземете някакъв елемент b от група Z a и разгледайте безкрайна последователност 1, b, b 2 , b 3 , b 4 , ... От факта, че група Z a е по дефиниция краен набор, рано или късно разглежданата последователност {b} ще започне да се повтаря. Задайте b i = b j (i <j).
Сега разделяме всяка част от равенството чрез b i (modulo a) и получаваме b ji = 1. Това означава, че има число k = ji, за което b k = 1 (mod a) е вярно. Най-малкото k, за което притежава това равенство, се нарича ред b. За да се избегне объркване с друга специална литература, стандартната математическа нотация се използва, за да се обясни системата Дифи-Хелман.
По този начин, увеличавайки числото b, наречено генериращ елемент, към силата, получаваме поредица от числа (множество) 1, ..., b k-1 . Броят на елементите в този набор е точно k.
Свойството на умножение по модул a казва, че съществува поне едно число b, което генерира всички елементи от групата Z * a . С други думи, има число, за което k = a - 1 е вярно.Това свойство ни позволява да представим числата на групата Z * a във вид 1, b, b 2 , ... b a-2 . Такова число b се нарича примитивен номер на група.
Впоследствие е лесно да се докаже от груповите признаци, че множеството, генерирано от числото b, също е само група и наследява всички свойства на групите. С други думи, операции в рамките на генерирана група или подгрупа могат да бъдат изпълнени по същия начин, както в група по модул а.
Помислете за изявлението. За всеки елемент b неговият ред е делител на a-1. Лесно е да се покаже. Нека a = 7. Числото b = 3 е примитивно, тъй като 1, ..., b 5 = 1, 3, 2, 6, 4, 5. Тогава числото h = 2 ще генерира подгрупа 1, ..., h 2 = 1 , 2, 4, тъй като h 3 = 2 3 mod 7 = 1. h = 6 генерира подгрупа 1, 6. Размерите на групите са съответно 3 и 2. Очевидно е, че те са делители на числото а-1 = 6.
Първият DH алгоритъм
В оригиналната версия алгоритъмът работи както следва. Голямо число а е избрано от множеството от прост и примитивен елемент b, генериращ Z * a . И двата числа a и b представляват публичния ключ, те са познати на всички, включително нападателите. Как тогава да се скрият съобщенията?
Именно на тази стъпка Дифи и Хелмън измислиха много изобретателен ход. Да предположим, че имаме двама души, които комуникират помежду си: А и Б. Първо, А избира случайно число x от Z * a , което е еквивалентно на избирането на число от {1, ..., a-1}. След това той изчислява стойността, използвайки формулата (b x mod a) и я изпраща на B. На свой ред, B избира определено число y от същия набор, изчислява стойността (b y mod a) и изпраща резултата обратно на A.
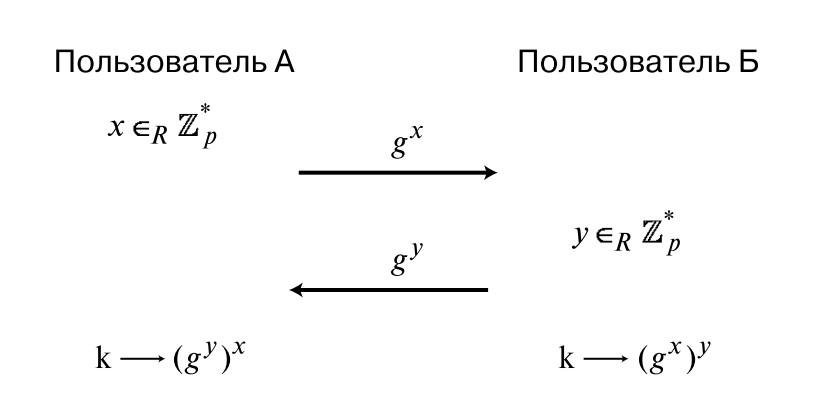
По такъв труден начин се оказва, че тайният ключ изглежда като b xy . Благодарение на свойството на градуси, което казва g xy = (g y ) x , събеседникът А може да изчисли желаната стойност и да дешифрира информацията, която му е изпратена. По същия начин тази стойност се изчислява от събеседника Б. И така, и двата имат един и същ секретен ключ.
Какви проблеми има един нарушител с този обмен на информация? Той може да пресече числата g x и g y . И дори с познаването на публичните ключове, проблемът за изчисляване на g xy не е тривиален, t. Тъй като не съществува ефективен алгоритъм за намиране на желаната стойност в разпределението на ключовете на Дифи-Хелман. Този проблем е известен като проблема за изчисляване на дискретен логаритъм.
Медиаторска атака
Една от слабостите на основния алгоритъм на Дифи-Хелман е неговата уязвимост срещу посреднически атаки. Какво означава това? Събеседник А знае, че комуникира с определено лице, но конкретно с кого - няма представа. Така нападателят може да проникне в трансфера на информация и да имитира събеседника Б, когато общува с А, и обратно. Никой от тях няма да може да подозира, че нещо не е наред.
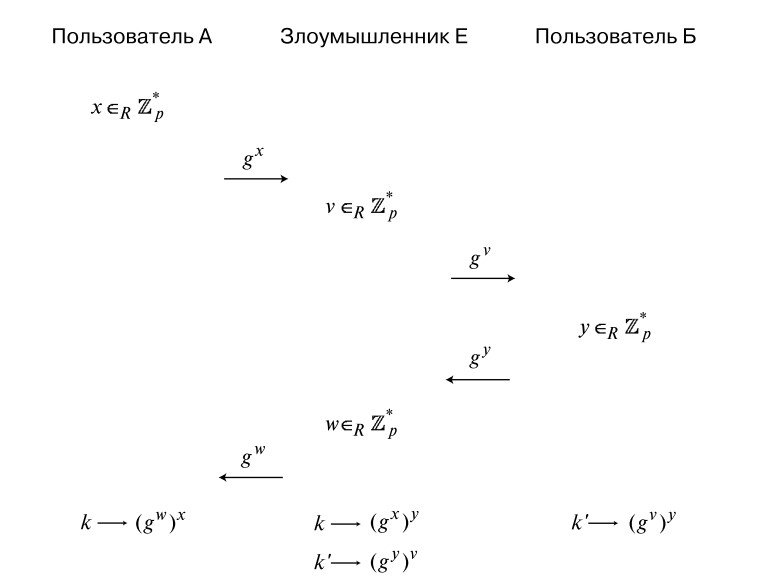
Има само една област на използване, в която атаките срещу алгоритъма Дифи-Хелман са изключени. Това е телефонно и видео повикване. Тук събеседниците са в състояние да се познават, така че медиаторът няма да може да проникне.
капани
В допълнение към атаката на медиаторите, протоколът DH съдържа множество други проблеми. Например, един от недостатъците е случаят, когато примитивът не е примитив. Тогава той генерира само една подгрупа. Поради стесняване на броя на възможните опции, нападателят отваря възможността за тяхното търсене.

Проблеми, дължащи се на този недостатък, могат да бъдат избегнати, ако всеки от събеседниците провери дали цифрите a и b са верни преди започване на обмена на данни. Това означава, че a е просто число, а b е примитивно. Въпреки това, когато става въпрос за сигурност чрез прилагането на някои еднакви, незадължителни стъпки, потребителите често ги игнорират.
Друг сериозен проблем възниква въз основа на подгрупи по модул а. Ако нападателят избере да промени g x на 1, за да му помогне по-лесно да подслушва, потребителите могат лесно да го открият, като проверят номера на съответствието. Ако обаче той замени ключа с номер на ниска поръчка, потребителите няма да могат да подозират нищо. И тъй като броят на елементите в комплекта с ниска поръчка ще бъде малък, нападателят ще трябва да оправи малък брой опции за декодиране.
Надеждност на простите числа
Алгоритъмът DH използва голям и надежден брой много прости. Как точно да го изберем? Анализираме стъпките.
- Използвайки формулата a = 2k + 1, изберете числата a и k, така че те да са прости.
- От множеството 1, ..., a-1 изключваме 1 и a-1.
- Вземете случайно число x от множеството, останало след втората стъпка и намерете стойността b = x 2 (mod a).
- Уверете се, че b не е равно на 1 или a-1. Ако b е равно на една от забранените стойности, трябва да изберете друг x. И повторете операцията.
Наборът (a, k, b), получен по този начин, може да се счита за достатъчен за използване в алгоритъма за обмен на ключове на Дифи-Хелман. Съответно, получателят на съобщението също трябва да провери стойността, която трябва да бъде сила на b, и да се увери (например, функция от символа Legendre), че попада в множеството, генерирано от числото b.
Използване на подгрупи
Основният недостатък на горния алгоритъм е недостатъчната ефективност. Ако приемем, че дължината на простото число a е n бита, тогава k е n-1 бита. Оказва се, че всички градуси ще бъдат n-1 дълги. Тогава операция степенуване средно ще се състоят от 3n / 2 умножения mod a. Това е доста голям процес.

За да се справим с този проблем, беше решено да се използват по-малки подгрупи. Каква е ползата от изпълнението в този случай? Ако числото a се състои от 2000 бита, тогава са необходими 3000 операции за умножение, за да се изчисли b x . Чрез използването на подгрупи, този брой може да бъде намален до ~ 400. Това значително увеличение на ефективността на алгоритъма прави възможно неговото пълно прилагане. Например, алгоритъмът Дифи-Хелман с три или повече членове.
Каква трябва да бъде дължината на a
Правилният избор на размерите на параметрите на алгоритъма Дифи-Хелман е доста сложна задача. Общо изискване в света на криптографията е, например, условието, че нападателят се нуждае от най-малко 2128 стъпки, за да проникне в системата. Ако в симетричните алгоритми за криптиране, за да се съобразят с такова изискване, е доста лесно, в алгоритмите с публичен ключ това е реален проблем. Ако отговаряте на горното изискване, тогава дължината a трябва да се състои от поне 850 байта.

На практика този размер създава големи проблеми с производителността в системата, тъй като операциите с публичен ключ отнемат много повече време, отколкото, например, в симетрично криптиране с 128 или 256 битови ключове. Тогава как да бъдем? Минималната дължина на публичния ключ трябва да започва от 2048 бита. Въпреки че колкото по-дълъг е ключът, толкова по-високо е нивото на защита. Трябва да се обърне внимание преди всичко на работата на системата и на нейните разходи. Ако ви позволява да използвате ключ от 4096 бита, трябва да го направите.
Как се оценява изискваното ниво на сигурност?
Размерите на ключовете в симетричното криптиране остават непроменени (128, 256 бита) през целия живот на системата, докато размерите на публичния ключ винаги са променлива стойност. Ако трябва да разработите система, която трябва да се използва в продължение на 30 години и да пазите данни в тайна поне 20 години след като системата бъде извадена от употреба, тогава размерът на симетричния ключ за криптиране трябва първоначално да е достатъчно голям, за да защити системата за следващите 50 години.
Поради очевидните проблеми с производителността, поради факта, че алгоритъмът на Дифи-Хелман криптира много по-голям брой операции, изискванията за публичните ключове се различават. Той остава валиден за една година и защитава данните за следващите 20 години, т.е. използва се общо 21 години. Поради променливия си размер, ключът може да се променя всяка година и да се създава все по-дълго, за да се гарантира необходимото ниво на сигурност.
Например, най-добрите оценки показват, че ключ с дължина от 256 байта може да осигури защита на данните в продължение на ~ 20 години, дължина от 384 байта е 35 години и с дължина от 512 байта е 47 години и т.н. Необходими са 2128 стъпки, за да се справят с него, получени от подобни оценки. Това обаче е само прогноза, на която трябва да се доверите с голяма грижа. Можете доста точно да предскажете развитието на събитията за 10 години напред, но при 50 - това е фантастично.
Практически препоръки
Ето някои практически съвети за използването на протокола DH. Изберете k като просто число от 256 бита. Това е минимумът, който може да осигури поне адекватно ниво на сигурност срещу атаките. За a изберете число, което би имало формата Na + 1, където N е цяло число. За размера на числото a беше казано по-рано. След това се избира случайно число b и се проверява за няколко условия. Първо, тя не може да бъде единица. Второ, b k = 1.
От своя страна всеки участник в комуникацията трябва да бъде убеден в следното:
- a и k са прости числа, дължината на k е 256 бита, дължината на p е доста голяма.
- числото k е делителят на a-1.
- b не е равно на 1 и b k = 1.
Тези условия трябва да бъдат проверени дори с безусловно доверие в източника.
заключение
Алгоритъмът DH е гениално решение на един от сериозните проблеми и все още се използва активно в модифицирана форма за съвременните изисквания за сигурност в различни протоколи. Алгоритъмът на Дифи-Хелман например се използва в някои части от изпълнението на IKE протокола. Въпреки това, използването му трябва да бъде методично и внимателно поради наличието на очевидни проблеми и сериозни капани.