Всички възможности за намиране на трапецовидната област
Многостранен трапецовид ... Може да бъде произволен, равнобедрен или правоъгълен. И във всеки случай, трябва да знаете как да намерите областта на трапеца. Разбира се, най-лесният начин да запомните основните формули. Но понякога е по-лесно да се използва това, което е извлечено с всички характеристики на конкретен геометрична форма.
Няколко думи за трапеца и нейните елементи
Всеки четириъгълник, чиито две страни са успоредни, може да бъде наречен трапец. Като цяло, те не са равни и се наричат бази. По-големият от тях е по-нисък, а другият е горен.
Другите две страни са странични. За произволен трапец те имат различна дължина. Ако те са равни, фигурата става равнобедрена.
Ако внезапно ъгълът между двете страни и основата е 90 градуса, то трапецът е правоъгълен.
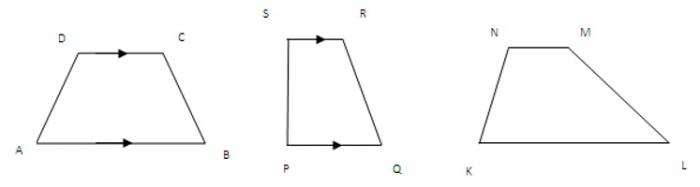
Всички тези характеристики могат да помогнат при решаването на проблема как да се намери площта на трапеца.
Сред елементите на фигурата, които могат да бъдат необходими за решаване на проблеми, можем да подчертаем следното:
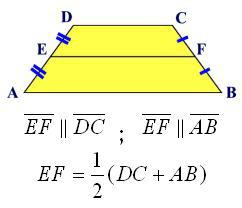
- отсечката, перпендикулярна на двете бази;
- средната линия, която с краищата си е средна страна.
С каква формула да се изчисли площта, ако знаете базата и височината?
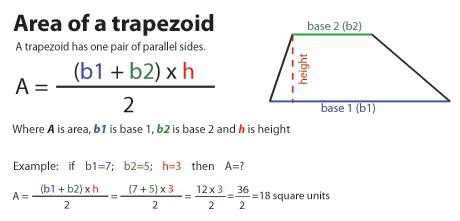
Този израз се дава от принципала, защото най-често можете да разпознавате тези стойности, дори когато не са посочени изрично. Така че, за да разберете как да намерите трапецовидна област ще трябва да сгънете двете бази и да ги разделите на две. След това получената стойност се умножава по стойността на височината.
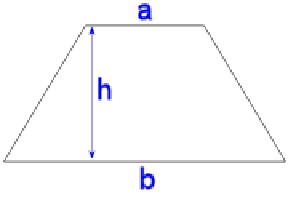
Ако обозначим базите с буквите a 1 и a 2 , височината е n, тогава формулата за областта ще изглежда така:
S = ((a 1 + a 2 ) / 2) * n.
Формулата за изчисляване на площта, ако е дадена нейната височина и средна линия
Ако се вгледате внимателно в предишната формула, лесно е да се види, че стойността на средната линия е явно в нея. А именно, сумата от базите, разделена на две. Нека средната линия се обозначава с буквата l, след това формулата за областта ще бъде така:
S = l * n.
Способността да се намери областта диагонално
Този метод ще ви помогне, ако знаете ъгъла, който се формира от тях. Да предположим, че диагоналите са обозначени с буквите q 1 и g 2 , а ъглите между тях са α и β. Тогава формулата за това как да се намери площта на трапеца ще бъде написана както следва:
S = ((d 1 * d 2 ) / 2) * sin α.
В този израз лесно можете да заместите α с β. Резултатът няма да се промени.
Как да открием района, ако всички страни на фигурата са известни?
Има и ситуации, когато точно в тази фигура са известни страни. Тази формула е тромава и трудна за запомняне. Но това е възможно. Нека страните имат обозначение: в 1 и 2 , основата и 1 повече от 2 . Тогава формулата за площ ще изглежда така:
S = ((a 1 + a 2 ) / 2) * √ {в 1 2 - [(a 1 - a 2 ) 2 + в 1 2 - в 2 2 ) / (2 * (a 1 - a 2 )) ] 2 }.
Начини за изчисляване на площта на равнобедрен трапец
Първият е свързан с факта, че в него може да се влезе кръг. И, знаейки неговия радиус (обозначен с буквата r), както и ъгъла в основата - γ, можете да използвате следната формула:
S = (4 * r 2 ) / sin γ.
Последната обща формула, която се основава на познанията на всички страни на фигурата, ще бъде значително опростена поради факта, че страните имат същото значение:
S = ((a 1 + a 2 ) / 2) * √ {в 2 - [(a 1 - a 2 ) 2 / (2 * (a 1 - a 2 ))] 2 }.
Методи за изчисляване на площта на правоъгълния трапец
Ясно е, че всеки от изброените за произволна форма ще свърши работа. Но понякога е полезно да се знае за една характеристика на такъв трапец. Тя се състои във факта, че разликата в квадратите на дължините на диагоналите е равна на разликата, съставена от квадратите на базите.
Често формули за трапец са забравени, докато изразите за областите на правоъгълник и триъгълник са запомнени. След това можете да приложите прост начин. Разделете трапецоида на две форми, ако е правоъгълна или три. Един точно ще бъде правоъгълник, а вторият или два оставащи триъгълника. След изчисляване на областите на тези цифри само ще ги добавите.
Това е доста прост начин как да намерим квадрат трапец.
Ами ако са известни координатите на върховете на трапеца?
В този случай ще трябва да използвате израз, който ви позволява да определите разстоянието между точките. Може да се приложи три пъти: за да научите и двете бази и една височина. И тогава просто приложите първата формула, която е описана малко по-високо.
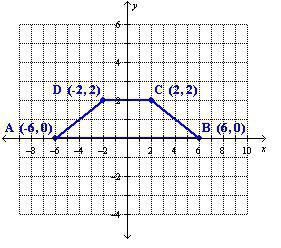
За да илюстрирате този метод, можете да дадете пример. Дадени са върховете с координатите А (5; 7), В (8; 7), С (10; 1), D (1; 1). Трябва да знаете областта на фигурата.
Преди да намерите областта на трапец, трябва да изчислите дължината на основата с координати. Ще ви е необходима следната формула:
дължина на сегмента = √ {(разлика на първите координати на точки) 2 + (разлика на вторите координати на точките) 2 }.
Горната база е обозначена с АВ, което означава, че нейната дължина ще бъде равна на √ {(8-5) 2 + (7-7) 2 } = =9 = 3. По-ниската ще бъде SD = √ {(10-1) 2 + (1-1) ) 2 } = =81 = 9.
Сега трябва да задържите височината от върха до основата. Неговото начало трябва да е в точка А. Краят на сегмента ще бъде на долната основа в точката с координати (5; 1), нека бъде точката N. Дължината на сегмента AN ще бъде равна на √ {(5-5) 2 + (7-1) 2 } = =36 = 6.
Остава само да замени получените стойности с формулата за трапецовидна област:
S = ((3 + 9) / 2) * 6 = 36.
Проблемът е решен без единици, защото координатната решетка не е зададена. Тя може да бъде или милиметър или метър.
Примери за задачи
№ 1. Състояние. Известен ъгъл между диагоналите на произволен трапец, той е равен на 30 градуса. По-малкият диагонал е 3 dm, а вторият е 2 пъти по-голям. Необходимо е да се изчисли площта на трапеца.
Решението. Първо трябва да знаете дължината на втория диагонал, защото без това не можете да преброите отговора. Изчислете, че е лесно, 3 * 2 = 6 (dm).
Сега трябва да използвате подходящата формула за района:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4.5 (dm 2 ). Проблемът е решен.
Отговор: площта на трапеца е 4,5 dm 2 .
№ 2. Състояние. В трапецовида на AVSD базите са AD и BC сегментите. Точка Е е средата на страната на СД. От него се извежда перпендикулярно на права линия А-В, краят на този сегмент се обозначава с буквата N. Известно е, че дължините AB и EH са съответно 5 и 4 см. Необходимо е да се изчисли площта на трапеца.
Решението. Първо трябва да направите рисунка. Тъй като стойността на перпендикуляра е по-малка от страната, към която се води, трапецовият слой ще бъде леко удължен нагоре. Така че EN ще бъде вътре във фигурата.
За да видите ясно напредъка на задачата, ще трябва да извършите допълнително строителство. А именно, начертайте права линия, която ще бъде успоредна на страната AB. Точките на пресичане на тази линия с AD - P и с продължаването на въоръжените сили - X. Получената цифра е паралелограма. Нещо повече, неговата площ е равна на желаната. Това се дължи на факта, че триъгълниците, които се оказаха с допълнителната конструкция, са равни. Това следва от равенството на страната и двата ъгъла, прилежащи към нея, една - вертикална, а другата - разположена напречно.
Да се намери зоната на паралелограма е възможно с формулата, която съдържа произведението на страната и височината, спуснати върху нея.
По този начин, площта на трапеца е 5х4 = 20 cm2.
Отговор: S = 20 cm 2 .
№ 3. Състояние. Елементите на равнобедрен трапец имат следните значения: долната основа е 14 см, горната е 4 см, а остър ъгъл е 45 °. Необходимо е да се изчисли площта му.
Решението. Нека по-малката база се определя като БЦ. Надморската височина от точка Б ще се нарича ВН. Тъй като ъгълът е 45º, триъгълникът ABH ще бъде правоъгълен и равнобедрен. И така, AN = BH. Освен това, НС е много лесно да се намери. Тя е равна на половината от основната разлика. Това е (14 - 4) / 2 = 10/2 = 5 (cm).
Основанията са известни, височината е отчетена. Можете да използвате първата формула, която се разглежда тук за произволен трапец.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (cm2).
Отговор: Необходимата площ е 45 см 2 .
№ 4. Състояние. Има произволен трапецовиден AVSD. От двете му страни се взимат точките О и Е, така че ОЕ е успоредно на основата на ковчега. Площта на трапецовида AOED е пет пъти по-голяма от тази на CFE. Изчислете OE стойността, ако дължините на основата са известни.
Решението. Необходимо е да се начертаят две успоредни AB равни линии: първата през точка C, пресечната точка с OE е точка T; втората през Е и точката на пресичане с AD ще бъде М.
Нека неизвестното OE = x. Височината на по-малкия трапецоид на CFE е n 1 ;
Тъй като областите на тези два трапеца са свързани с 1 до 5, можем да напишем следното равенство:
(x + a 2 ) * n 1 = 1/5 (x + a 1 ) * n 2
или
n 1 / n 2 = (x + a 1 ) / (5 (x + a 2 )).
Височините и страните на триъгълниците са пропорционални по конструкция. Затова можем да напишем друго равенство:
n 1 / n 2 = (x - a 2 ) / (a 1 - x).
В последните два записа от лявата страна има равни стойности, така че можете да напишете, че (x + a 1 ) / (5 (x + a 2 )) е равно на (x - a 2 ) / (a 1 - x).
Това изисква серия от трансформации. Първо умножете напречно. Ще се появят скоби, които показват разликата в квадратите.След прилагането на тази формула ще получите кратко уравнение.
Необходимо е да отворите скобите и да преместите всички термини от неизвестното "х" в лявата страна, след което извлечете квадратен корен.
Отговор : x = √ {(a 1 2 + 5 a 2 2 ) / 6}.